Пошаговое объяснение:
Выясним, при каких значениях переменной функция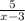 
не определена.
R ( x ) =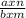 
, где n - степень числителя, а m - степень знаменателя.
Если n < m , то ось x, y = 0 , является горизонтальной асимптотой.
Если n = m , то горизонтальной асимптотой является прямая y = a b .
Если n > m , то не существует горизонтальной асимптоты (только наклонная асимптота).
Найдем n и m .
n = 0
m = 1
n < m , ось X, y = 0 , является горизонтальной асимптотой. y = 0
Вертикальные асимптоты: x = 3
Горизонтальные асимптоты: y = 0
Нет наклонных асимптот.
Находим частные производные первого порядка функции трёх переменных u
по х: 2х/(уz²); по у: -x²/(y²z²); по z: -2х²/(уz³);
получаем (2х/(уz²))*→i+ ( -x²/(y²z²))*→j -(2х²/(уz³))*→k; подставляем координаты точки М ,получаем 12*→i-12*→j -12√6*→k;
Аналогично находим частные производные первого порядка функции трёх переменных v:
по х: 3х²/2; по у: 18y²; по z: 9√6z²; подставляем координаты точки М ,получаем 3→i+9*→j +3√6*→k;
найдем скалярное произведение полученных векторов
12*3-12*9 -12√6*3√6=36-108-216=-288;
√(144+144+144*6)=12√8=24√2
и √(9+81+9*6)=√144=12
cosα=-288/(24√2*12)=-12/(12√2)=-1/(√2)=-√2/2, значит, угол между векторами равен 180°-45°=135°
Понятно, что всего четырехзначных чисел 9999 - 999 = 9000.
Вспомним какие числа делятся на 5. Число делится на 5 тогда и только тогда, когда последняя цифра 5 или 0. В нашем случае фиксируем цифру 5 на последнее место четырехзначного числа.
_ _ _ 5
а) Вопрос: сколькими можно составить четырехзначные числа из цифр 3,4,5,6,7,8, кратные 5, если цифры не повторяются?
На первое место используются любые цифры из пяти (3, 4, 6, 7, 8). На второе место — оставшиеся из четырех цифр, а на третье место — оставшиеся из трех цифр. Таких четырехзначных чисел составить можно
Вероятность того, что случайным образом выбранное число, делится на 5, если цифры не повторяются, равна 60/9000 = 2/300
б) Аналогично ставим вопрос такой же, только, если цифры повторяются.
На первые три места используются любые цифры из шести заданных, а на четвертом месте - одна цифра 5. Таких четырехзначных чисел можно составить 6³ * 1 = 216
Вероятность того, что случайным образом выбранное число, делится на 5, если цифры повторяются, равна 216/9000 = 3/125 = 0.024