Укажите словосочетание а)весьма искусный б)менее грузный в)согласно распоряжению г)самый масштабный д)более интересный

👇

Увидеть ответ

Ответ:

мошкада

11.04.2020

В) согласно распоряжению, так как здесь есть и наречие и зависимое к нему слово

4,8(17 оценок)

Открыть все ответы

Ответ:

Olga200393

11.04.2020

Написать уравнение касательной и нормали к графику функции f(x)=x^4/4-27x+60 в точке х₀=2.

ответ:

Уравнение касательной имеет вид y=48-19x.

Уравнение нормали имеет вид y=188/19+х/19.

Пошаговое объяснение:

Вспомним общий вид уравнения касательной:

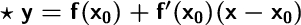
$\Large \boldsymbol {} \text{ $ \boldsymbol{\sf \star \ y=f(x_0)+f'(x_0)(x-x_0)}$ \boldsymbol}$

И общий вид уравнения нормали:

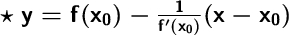
$\Large \boldsymbol {} \text{ $ \boldsymbol{\sf \star \ y=f(x_0)-\frac{1}{f'(x_0)}(x-x_0)}$ \boldsymbol}$

1. Найдём f(x₀).

Для этого в функцию вместо переменной х подставляем значение х₀=2.

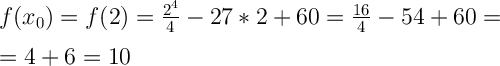
$\Large \boldsymbol {} f(x_0)=f(2)=\frac{2^4}{4}-27*2+60=\frac{16}{4} -54+60==4+6=10$

2. Найдём производную функции.

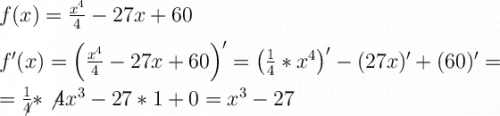
$\Large \boldsymbol {} f(x)=\frac{x^4}{4}-27x+60f'(x)=\left(\frac{x^4}{4}-27x+60\right)'=\left(\frac{1}{4}*x^4\right)'-(27x)'+(60)'==\frac{1}{\not4}*\not4x^3-27*1+0=x^3-27$

3. Найдём f'(x₀).

Для этого в производную функции вместо переменной х подставляем значение х₀=2.

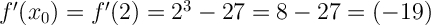
$\Large \boldsymbol {} f'(x_0)=f'(2)=2^3-27=8-27=(-19)$

4. Записываем уравнение касательной.

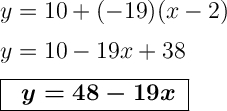
Для этого имеющиеся значения f(x₀), f'(x₀) и x₀ подставляем в вышеуказанную формулу уравнения касательной.

$\Large \boldsymbol {} y=10+(-19)(x-2)y=10-19x+38boxed{ \text{ $ \boldsymbol{ \ y=48-19x}$ \boldsymbol}}$

5. Записываем уравнение нормали.

Для этого имеющиеся значения f(x₀), f'(x₀) и x₀ подставляем в вышеуказанную формулу уравнения нормали.

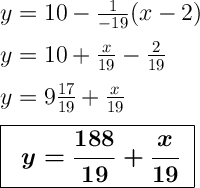
$\Large \boldsymbol {} y=10-\frac{1}{-19} (x-2)y=10+\frac{x}{19} -\frac{2}{19}y=9\frac{17}{19} +\frac{x}{19} }boxed{ \text{ $ \boldsymbol{ \ y=\frac{188}{19} +\frac{x}{19} }$ \boldsymbol}}$

4,6(39 оценок)

Ответ:

artemy050702

11.04.2020

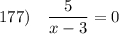
$177)\ \ \ \dfrac{5}{x-3}=0$

Если дробь равна 0 , то её числитель должен равняться 0, а знаменатель не может равняться 0 .

Если в числителе записано число 5, которое не равно 0, то числитель в 0 не обращается . Поэтому уравнение не имеет решений .

б)

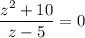
$\dfrac{z^2+10}{z-5}=0$

В числителе написано выражение, которое при любых значениях переменной будет больше 0 , и никогда в 0 не обратиться, так как

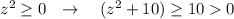$z^2\geq 0\ \ \to \ \ \ (z^2+10)\geq 10 0$ . Поэтому уравнение не имеет решений .

в)

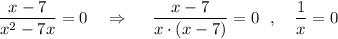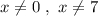$\dfrac{x-7}{x^2-7x}=0\ \ \ \Rightarrow \ \ \ \ \dfrac{x-7}{x\cdot (x-7)}=0\ \ ,\ \ \ \dfrac{1}{x} =0$ , причём $x\ne 0\ ,\ x\ne 7$ .

После упрощения выражения в левой части равенства получили дробь, в числителе которой стоит число 1 . Числитель не равен 0 . Поэтому уравнение не имеет решений .

4,5(13 оценок)

Это интересно:

Хобби-и-рукоделие

18.04.2021

Как сшить жилетку: подробный мастер-класс...

Мир-работы

10.10.2021

Как стать дрессировщиком дельфинов: руководство для начинающих...

Взаимоотношения

19.03.2022

Как прийти в себя после разрыва отношений...

Кулинария-и-гостеприимство