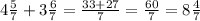Длина прямоугольника равна 13 см.
Пошаговое объяснение:
Пусть х - ширина прямоугольника, тогда (х+3) - длина прямоугольника.
Площадь прямоугольника равна (х+3)*х см²
После увеличения длины на 2 см и ширины на 1 см, измерения прямоугольника стали равны: длина х+3+2=х+5 (см) , ширина х+1 (см).
Площадь полученного прямоугольника равна (х+5)(х+1) см².
По условию, площадь полученного прямоугольника больше площади исходного прямоугольника на 35 см². Составим уравнение:
(х+5)(х+1)=(х+3)*х=35
x²+6x+5=x²+3x+35
6x-3x=30-5
3х=30
х=30:3
x=10 (см) - ширина прямоугольника
х+3=10+3=13 (см) - длина прямоугольника
Задача.
Решение, по заданию (уравнением):
210:3=x
x = 210:3
x = 70 (т.)
Проверка:
210:3=70 (т.)
Для начальной школы:
210:3 = x
x = 310:3
x = 70 (т.)
—————
210:3 = 70 (т.)
ответ: 70 тенге.
Решение, как второй вариант:
210:3=70 (т.) - стоит килограмм картофеля.
ответ: килограмм картофеля стоит 70 тенге.
Удобнее будет номер один, так как заместо " x" поставить другое число не получится. Но более сжатым вариантом будет вариант "2".
Также есть вариант решение уравнением, в таком виде:
3x=210
x=210:3
x=70 (т.)
Проверка:
3•70=210
(Хотя в таких случаях, обычно, проверка не пишется)
Тогда, более понятным будет 2-ой вариант. Ведь с таковым родом уравнения можно запутаться. Но такие уравнения пишутся в средней школе.
1)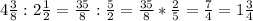
2)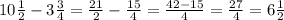
3)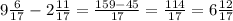
4)