1. Найдите значение производной функции в точке x₀:
a) y=(3·x-2)⁷, x₀=3
y'=((3·x-2)⁷)'=7·(3·x-2)⁶·(3·x-2)'=7·(3·x-2)⁶·3=21·(3·x-2)⁶
y'(3)=21·(3·3-2)⁶=21·7⁶=21·117649=2470629
б) y=(4-5·x)⁷, x₀=1
y'=((4-5·x)⁷)'=7·(4-5·x)⁶·(4-5·x)'=7·(4-5·x)⁶·(-5)= -35·(4-5·x)⁶
y'(1)= -35·(4-5·1)⁶= -35·(-1)⁶= -35·1= -35
в) y=(2·x+3)⁵, x₀=2
y'=((2·x+3)⁵)'=5·(2·x+3)⁴·(2·x+3)'=5·(2·x+3)⁴·2=10·(2·x+3)⁴
y'(2)=10·(2·2+3)⁴=10·7⁴=10·2401=24010
г) y=(5-3·x)⁷, x₀=1
y'=((5-3·x)⁷)'=7·(5-3·x)⁶·(5-3·x)'=7·(5-3·x)⁶·(-3)= -21·(5-3·x)⁶
y'(1)= -21·(5-3·1)⁶= -21·2⁶= -21·64= -1344
2. Вычислить скорость изменения функции в точке x₀ (скорость изменения равносильно производная первого порядка):
a) y=(2x+1)⁵, x₀= -1
y'=((2·x+1)⁵)'=5·(2·x+1)⁴·(2·x+1)'=5·(2·x+1)⁴·2=10·(2·x+1)⁴
y'(-1)=10·(2·(-1)+1)⁴=10·(-1)⁴=10·1=10
б) 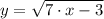 , x₀= 1
, x₀= 1


в)  , x₀= 2
, x₀= 2 
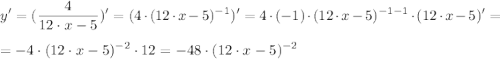

г) 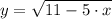 , x₀= -1
, x₀= -1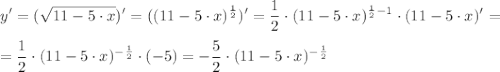
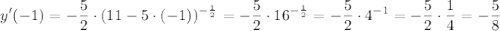
3. Найдите производные функций:
a) y=(x-1)·(x²+x+1) = x³-1
=1·(x²+x+1)+(x-1)·(2·x+1)= x²+x+1+2·x²+x-2·x-1 =3·x²
б) 

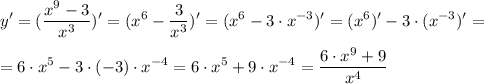
Пусть прыжки по часовой стрелке обозначаются со знаком "плюс", а против часовой стрелке - со знаком "минус".
Найдем, какие более простые прыжки с точки зрения перемещения (то есть по модулю) можно совершить.
Изначально имеется два прыжка (+21) и (-15) Выполним их по очереди:
Итак, каким-то образом можно выполнить прыжок (+6).
Сгруппируем прыжки (+6) и (-15):
Таким образом, можно выполнить прыжок (-9).
Наконец, сгруппируем прыжки (+6) и (-9):
Также выполним прыжок (-3).
Получить прыжок с меньшим перемещением (кроме тривиально нулевого) невозможно.
Обратим внимание на то, что общее число каменей 2019, а также все рассмотренные прыжки кратны 3. Это означает, что при любом прыжке номер исходного и номер конечного камня дают одинаковые остатки при делении на 3.
Посетить все камни с номерами, дающими при делении на 3 один и тот же остаток, можно. У нас есть прыжок (-3).
Таким образом, мы посещаем либо все камни с номерами, кратными 3, либо все с номерами, дающими при делении на 3 остаток 1, либо все с номерами, дающими при делении на 3 остаток 2. И тех и других и третьих поровну в количестве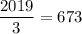 штуки.
штуки.
ответ: 673