Question

Решить (выш.мат.) больному делается инъекция в момент времени t=0. концентрация лекарственного препарата в крови в момент времени t описывается зависимостью , где a> 0, b> 0. определить момент времени, когда концентрация достигнет максимума.

Answer 1

Вычисляем производную:

$c'=c_0(be^{-bt}-ae^{-at})$

В момент времени t = 0 концентрация c(0) = 0, производная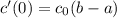 $c'(0)=c_0(b-a)$. Концентрация не может быть отрицательной, поэтому осмысленным ситуациям соответствует ситуация b > a (считаю, что $c_00$).

Найдём, при каком t производная равна нулю:

$c_0(be^{-bt}-ae^{-at})=0\\e^{(b-a)t}=\dfrac ba\\t=\dfrac{\ln (b/a)}{b-a}$

При b > a вычисленное значение t > 0, при меньших t производная c' > 0, при больших - c' < 0, значит, при этом t достигается максимум.

$\boxed{t=\dfrac{\ln (b/a)}{b-a}}$