
Итак, найти нужно площадь криволинейной трапеции, заключённой между данными линиями.
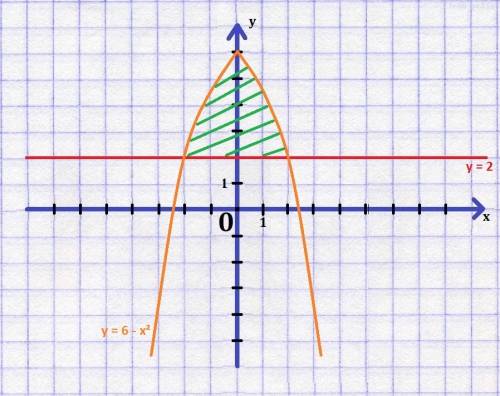
1) Для решения таких задач, в первую очередь нужно построить график.
Расписывать построение я не буду, раз решаете задачи с интегралами, графики прямой и параболы изобразить не проблема.
График смотри в приложении.
2) По графику видно, что ![x \in [-2; 2]](/tpl/images/0956/7693/ec99f.png) , это и будут наши пределы интегрирования.
, это и будут наши пределы интегрирования.
3) Если на отрезке ![[-2; 2]](/tpl/images/0956/7693/e848a.png) непрерывная функция
непрерывная функция 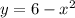 больше либо равна непрерывной функции
больше либо равна непрерывной функции 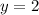 , то площадь фигуры, ограниченной графиками данных функций и прямыми
, то площадь фигуры, ограниченной графиками данных функций и прямыми 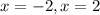 , можно найти так:
, можно найти так: 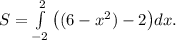
4) Вычислим полученный интеграл.
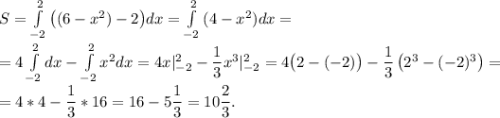
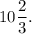
а) 308 м, 247,5 м, 209м
б) В 5,5 раз.
Пошаговое объяснение:
а) Раз треугольники подобны, то их стороны по определению пропорциональны.
Давайте для наглядности обозначим эти два треугольника буквами : первый пускай будет △ABC, а второй — △DEF. В таком случае можно сделать такую запись: △ABC ~ △DEF (знак тильда должен находиться на уровне букв).
Теперь составляем такую запись : 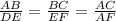
Подставляем известные стороны : 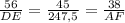
И вычисяем две неизвестные стороны второго треугольника :
1 :
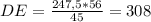 м
м
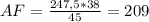 м
м
2 (через коэффициент пропорциональности) :
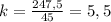
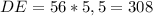 м
м
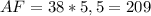 м
м
ответ : Остальные две стороны второго треугольника равны 308 м и 209 м.
б) P(△ABC) = 45 + 56 + 38 = 139 м
P(△DEF) = 308 + 247,5 + 209 = 764,5 м
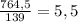
ответ : Периметры участков отличаются в 5,5 раз (тот же коэффициент пропорциональности).