Question

100 ! ! исследовать на сходимость ряды 1) сума от 1 до бесконечности 1/(n^2 +2n +3) 2) сума от 1 до бесконечности sin(pi/2^n) 3) сума от 1 до бесконечности 1/(2n+1)!

Answer 1

ответ: 1) сходится 2) сходится 3) сходится

Пошаговое объяснение:

1) Известно, что ряд сумма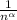 $\frac{1}{n^{\alpha }}$ сходится при α > 1

В частности сходится и ряд суммы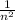 $\frac{1}{n^{2}}$

Т.к.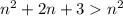 $n^{2}+2n+3n^{2}$

то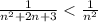 $\frac{1}{n^{2}+2n+3}$

По признаку сравнения для положительных числовых рядов из сходимости ряда с большими членами следует сходимость ряда с меньшими членами.

2) Аргумент синуса убывает от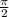 $\frac{\pi }{2}$ для 0

Следовательно рассматриваемый ряд положителен и для синуса можем записать

sinx < x

Исследуем на сходимость ряд сумм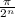 $\frac{\pi }{2^{n}}$

Найдем для него отношение последующего члена к предыдущему

$D=\frac{\frac{\pi}{2^{n+1}}}{\frac{\pi}{2^{n}}}=\frac{1}{2}$

По признаку Даламбера ряд сумм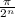 $\frac{\pi }{2^{n}}$ сходится.

По признаку сравнения для положительных числовых рядов из сходимости ряда с большими членами следует сходимость ряда с меньшими членами, т.е сходится и ряд сумм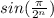 $sin(\frac{\pi}{2^{n}})$

3. Найдем отношение последующего члена к предыдущему

$D=\frac{\frac{1}{(2n+3)!}}{\frac{1}{(2n+1)!}}=\frac{1}{(2n+2)(2n+3)}$

При n стремящемся к бесконечности D стремится к нулю, а следовательно, по признаку Даламбера ряд сходится.