Первое число 15, второе 9
Пошаговое объяснение:
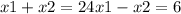
Дальше отнимаем первое и второе уравнение и получаем ответ
Пошаговое объяснение:
Задание1
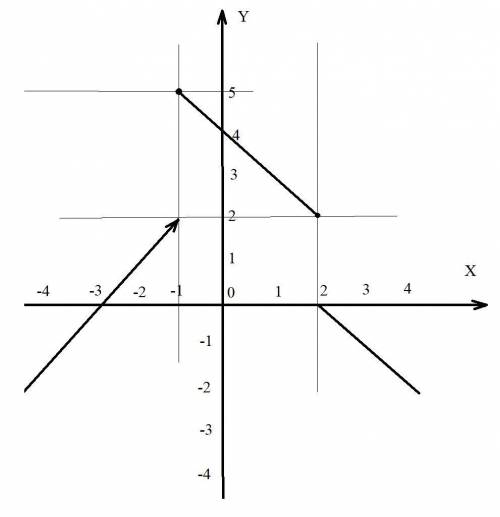
Решение в чертеже. Но в условии есть некорректное значение относительно значения х=2. В одном из неравенств области определения х должно быть строгое неравенство.
Задание 2
Решить уравнения
1) sin(x/2) = - 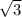 /2
/2
x/2 = - /2 ±
/2 ±  /6 + 2
/6 + 2 k
k
x = - ±
± /3 + 4
/3 + 4 k
k
ответ x = ± /3 +
/3 +  (4k-1)
(4k-1)
2) 2sin(x+ /5) =
/5) = 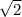
sin(x+ /5) =
/5) = 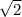 /2
/2
x+ /5 =
/5 =  /2 ±
/2 ±  /4+2
/4+2 k
k
x = ± /4+
/4+ /2-
/2- /5+2
/5+2 k
k
ответ x = ± /4+
/4+ 3/10+2
3/10+2 k
k
3) -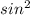 x + 2sinx -1 = 0
x + 2sinx -1 = 0
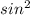 x - 2sinx +1 = 0
x - 2sinx +1 = 0
пусть y=sinx тогда
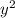 - 2y +1=0
- 2y +1=0
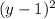 =0
=0
y = 1
sinx = 1
x= /2 + 2
/2 + 2 k
k
4) 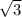 sinx + cosx = 0
sinx + cosx = 0
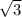 tgx + 1 = 0
tgx + 1 = 0
tgx = -1/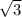
x= - /6 +
/6 +  k
k
5) cos5x = cos3x
cos(4x+x) = cos(4x-x)
cos(4x+x) = cos4x cosx - sin4x sinx
cos(4x-x) = cos4x cosx + sin4x sinx
cos4x cosx - sin4x sinx = cos4x cosx + sin4x sinx
2sin4x sinx =0
sin4x = 0 или sinx = 0
тогда
4x=pk или x=pk
следовательно
решениями являются x=pk/4 и x=pk
(4s)/v часов.
Пошаговое объяснение:
s = v * t ⇒ t = s / v
Время, затрачиваемое при подъёме по пути из пункта A в пункт B:
t₁ = s / v
Время, затрачиваемое при спуске по пути из пункта A в пункт B:
t₂ = 2s / 2v = s / v
Время, затрачиваемое на весь путь из пункта A в пункт B:
t₃ = t₁ + t₂ = ( s / v ) + ( s / v ) = 2 * ( s / v ) = ( 2s ) / v
Спуск по пути из пункта A в пункт B становится подъёмом по пути из пункта B в пункт A.
Время, затрачиваемое при подъёме по пути из пункта B в пункт A:
t₄ = s / v
Время, затрачиваемое при спуске по пути из пункта B в пункт A:
t₅ = 2s / 2v = s / v
Время, затрачиваемое на весь путь из пункта B в пункт A:
t₆ = t₄ + t₅ = ( s / v ) + ( s / v ) = ( 2s ) / v
Время, затрачиваемое на путь из пункта A в пункт B и обратно:
t = t₃ + t₆ = ( 2s ) / v + ( 2s ) / v = ( 2s + 2s ) / v = ( 4s ) / v (ч)
1) (24-6) : 2=9 меньшее частное или слагаеммое
2) 9+6=15 большее частное или слагаеммое
Пошаговое объяснение: