Дано: Y(x) = (x²+6*x-9)/(x+4)
Исследование:
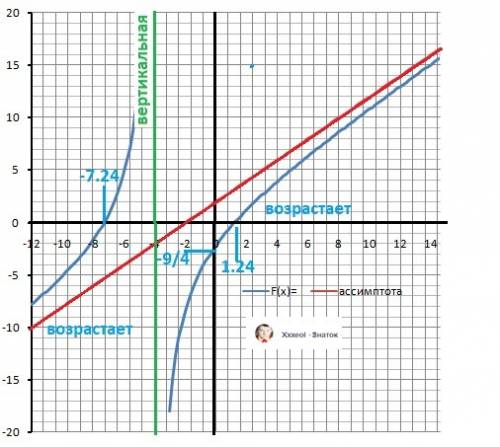
Рисунок с графиком в приложении.
1. Область определения: D(y)= X≠ -4 , X∈(-∞;-4)∪(-4+∞); Не допускаем деления на 0 в знаменателе.
2. Разрыв при Х = -4. Вертикальных асимптота - Х = -4 - зелёная.
3.Поведение на бесконечности. Y(-∞)= -∞, Y(+∞)= +∞ - горизонтальной асимптоты - нет.
4. Нули функции, пересечение с осью ОХ. Решаем квадратное уравнение в числителе.
x² + 6*x - 9 = 0. D= 72, X1 = 1.24, X2 = - 7.24 - нули функции.
. 5. Интервалы знакопостоянства.
Отрицательна: Y(x)<0 - X∈(-∞;-7,24)∪(-4;1,24)
Положительна: Y>0 - X∈(-7,24;-∞)∪(1,24;+∞;)
6. Проверка на чётность. Есть сдвиг по оси ОХ - нет симметрии ни осевой ни центральной.
Функция ни чётная: Y(-x) ≠ Y(x), ни нечётная: Y(-x) ≠ -Y(x)
7. Поиск экстремумов по первой производной.
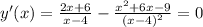
Корней нет. Экстремумов - нет.
8. Интервалы монотонности.
Возрастает - X∈(-∞;-4)∪(-4+∞) - везде где существует.
9. Поиск перегибов по второй производной.
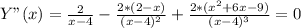
Точки перегиба нет, кроме разрыва при Х = -4.
10. Вогнутая - "ложка"- X∈(-∞;-4), выпуклая - "горка" X∈(-4;+∞);
11. Наклонная асимптота.
k = lim(+∞) Y(х)/x = (x²+6*x-9)/(x² - 4*x) = 1 - разделили и числитель и знаменатель на х².
b = lim(+∞) Y(x) - x = [x²+6x-9 - (x²- 4x)]/(x-4) = (10*x- 5)/(x-4) (??? = 2).
12. Область значений. E(y) = (-∞;+∞).
((5/12)-х)×2=(2/9)
(5/6)-2х=(2/9)|×18
(3×6×5)/6-2х×18=(2×2×9)/9
3×5-36х=2×2
15-36х=4
-36х=4-15
-36х=-11|÷(-36)
х=(-(-11)/36)
х=11/36
проверка:
((5/12)-(11/36)÷1/2=2/9
((5×3-11)/36)×2=2/9
((15-11)/36)×2=2/9
4/18=2/9
2/9=2/9-истина.
2) (1(16/25)+х)-(4/5)=4(2/25)
(41/25)+х=(102/25)+(4/5)
(41/25)+х=(102+4×5)/25
(41/25)+х=(102+20)/25
(41/25)+х=(122/25)
х=(122/25)-(41/25)
х=(122-41)/25
х=81/25
х=3(6/25)
проверка:
(1(16/25)+3(6/25))-(4/5)=4(2/25)
(41+81)/25-(4/5)=(102/25)
((122-4×5)/25)=(102/25)
((122-20)/25)=(102/25)
(102/25)=(102/25)-истина