Question

Числа p и q подобраны так, что парабола y=qx−x2 пересекает гиперболу xy=p в трёх различных точках a,b и c, причём сумма квадратов сторон треугольника abc равна 378, а точка пересечения его медиан находится на расстоянии 3 от начала координат. найдите произведение pq. ответ дайте в виде действительного числа, округлив его при необходимости стандартным образом до сотых. целую и дробную части разделяйте точкой. если возможных различных значений произведения pq окажется несколько, в ответе укажите их сумму.

Answer 1

pq = 54

Пошаговое объяснение:

Пусть точки пересечения имеют вид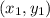 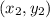$(x_1,y_1)$, $(x_2,y_2)$ и $(x_3,y_3)$. Выразим через координаты то, что дано в условии.

Сумма квадратов сторон:

$(x_1-x_2)^2+(y_1-y_2)^2+(x_2-x_3)^2+(y_2-y_3)^3+(x_3-x_1)^2+\\+(y_3-y_1)^2=2(x_1^2+y_1^2+x_2^2+y_2^2+x_3^2+y_3^2)-2(x_1x_2+x_2x_3+\\+x_3x_1+y_1y_2+y_2y_3+y_3y_1)=2a-2b=378$

(a - сумма квадратов, b - сумма попарных произведений)

Расстояние от начала координат до точки пересечения медиан

Известно, что координаты точки пересечения медиан можно найти по формулам:

$x_0=\dfrac{x_1+x_2+x_3}3\\y_0=\dfrac{y_1+y_2+y_3}3$

Тогда квадрат расстояния от начала координат до точки пересечения медиан, для удобства умноженный на 9, выражается так:

$9(x_0^2+y_0^2)=(x_1+x_2+x_3)^2+(y_1+y_2+y_3)^2=a+2b=9\cdot3^2=81$

Получилась система линейных уравнений на a и b. Из неё 4b = 2 * 81 - 378 = -216, b = -54. Осталось выразить сумму попарных произведений, для этого понадобится немного преобразовать систему и вспомнить теорему Виета.

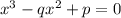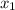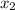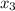Умножаем уравнение параболы на x и заменяем xy на p, получается кубическое уравнение $x^3-qx^2+p=0$. Понятно, что найдя из этого уравнения x, потом по формуле y = p/x однозначно найдем y. Значит, $x_1$, $x_2$ и $x_3$ - корни кубического уравнения. По теореме Виета сумма их попарных произведений равна коэффициенту при x, он равен нулю.

Умножаем уравнение параболы на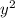 $y^2$, избавляемся от x и получаем 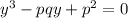$y^3-pqy+p^2=0$. Аналогично, нужна сумма попарных произведений, она равна -pq.

Приравниваем:

$-54=b=(x_1x_2+x_2x_3+x_3x_1)+(y_1y_2+y_2y_3+y_3y_1)=0-pq\\pq=54$