Question

Нужно решение к ! ,молю 1.отношение кубов больших полуосей орбит двух астероидов равно 25.во сколько раз период обращения одного астероида больше периода обращения другого. 2.отношение квадратов периодов обращения двух небесных тел вокруг солнца равно 125.во сколько раз большая полуось орбиты одного тела меньше большой полуоси орбиты другого тела. 3.минимальное расстояние от солнца до кометы равно 0,8а.е.,а максимальное 8,2а.е.чему равна большая полуось орбиты кометы

Answer 1

1. Третий закон Кеплера гласит, что квадраты периодов обращения тел относятся как кубы больших полуосей орбит этих тел. По условию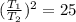 $(\frac{T_{1} }{T_{2} } )^{2}=25$. Значит, отношение периодов равно: $\frac{T_{1} }{T_{2} }=\sqrt{25}=5$.

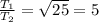ответ: в 5 раз.

2. Используем всё тот же третий закон Кеплера. По условию: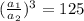 $(\frac{a_{1} }{a_{2} } )^{3}=125$. Значит, отношение больших полуосей этих тел равно: $\frac{a_{1} }{a_{2} }=\sqrt[3]{125}=5$.

ответ: в 5 раз.

3. Космические тела (в т. ч. кометы) движутся вокруг звёзд по эллиптическим орбитам, причём звезда находится в одном из фокусов эллипса. Минимальное расстояние от кометы до Солнца -- это расстояние от фокуса до вершины эллипса, а максимальное расстояние -- это расстояние от фокуса до противоположной вершины. Минимальное и максимальное расстояния лежат на одной прямой, которая называется большой осью эллипса. Соответственно, большая полуось равна половине большой оси эллипса. Для её нахождения нужно сложить максимальное и минимальные расстояния до Солнца и разделить эту сумму на два: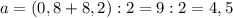 $a=(0,8+8,2):2=9:2=4,5$ а. е. .

ответ: 4,5 а. е. .