Боковые стороны трапеции равны по 8 см.
Пошаговое объяснение:
Трапеция называется равнобокой, если ее боковые стороны равны.
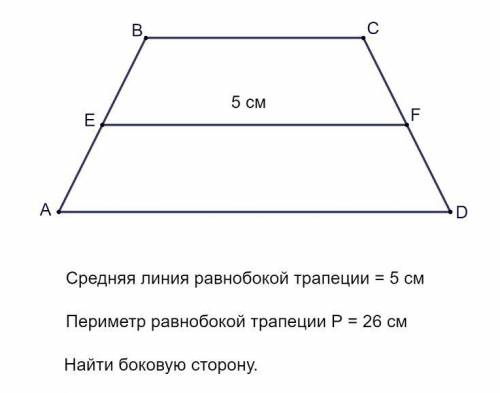
Пусть дана равнобокая трапеция ABCD. Ее боковые стороны равны AB = CD. Средняя линия EF = 5 см.
Средняя линия трапеции - это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции равна полусумме оснований.
EF =  см
см
BC + AD = 2 * 5 = 10 (см)
Периметр равен сумме длин всех сторон, P = 26 см.
Сумма боковых сторон трапеции: AB + CD = P - (BC + AD) = 26 - 10 = 16 (см).
Боковые стороны: AB = CD = 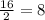 (см).
(см).
5х^2-4х-5х+4=0
х(5х-4)-(5х-4)=0
(5х-4)(х-1)=0
5х-4=0 => х= 4/5(дробь)
х-1=0 => х=1
2)4х^2+8х-21=0
4х^2+14х-6х-21=0
2х(2х+7)-3(2х+7)=0
(2х+7)(2х-3)=0
2х+7=0 => х= - 2/7(дробь)
2х-3=0 => х= 3/2(дробь)
1) 10х^2+8х-12,8=0
10х^2+8х - 64/5(дробь)=0 надо умножить обе части на 5
50х^2+40х-64=0
25х^2+20х-32=0
25х^2+40х-20х-32=0
5х(5х+8)-4(5х+8)=0
(5х+8)(5х-4)=0
5х+8=0 => х= -8/5(дробь)
5х-4=0 => х= 4/5(дробь)