ответ: (2, -1, 1)
Пошаговое объяснение: Запишем систему уравнений в матричном виде.
![\left[\begin{array}{cccc}3&-1&2&9\\2&3&-1&0\\2&4&3&3\end{array}\right]](/tpl/images/1055/0577/e1322.png)
Приведем к ступенчатому виду. Применяем операцию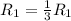 
к 
(к 1 строке) для того, чтобы сделать некоторые элементы строки равными 1.
![\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\2&3&-1&0\\2&4&3&3\end{array}\right]](/tpl/images/1055/0577/6eddc.png)
Применяем операцию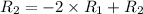 
к 
(ко 2 строке) для того, чтобы сделать некоторые элементы строки равными 0.
Применяем операцию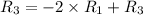 
к 
(к 3 строке) для того, чтобы сделать некоторые элементы строки равными 0.
![\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\0&\frac{11}{3} &-\frac{7}{3}&-6 \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]](/tpl/images/1055/0577/0d2b8.png)
Применяем операцию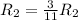 
к для того, чтобы сделать некоторые элементы строки равными 1.
![\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\0&1&-\frac{7}{11} &-\frac{18}{11} \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]](/tpl/images/1055/0577/8a8f7.png)
Применяем операцию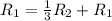 
к для того, чтобы сделать некоторые элементы равными 0.
![\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]](/tpl/images/1055/0577/c212b.png)
Применяем операцию 
к для того, чтобы сделать некоторые элементы строки равными 0.
![\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&\frac{51}{11} &\frac{51}{11} \end{array}\right]](/tpl/images/1055/0577/960ac.png)
Применяем операцию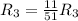 
к для того, чтобы сделать некоторые элементы строки равными 1.
![\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&1 &1 \end{array}\right]](/tpl/images/1055/0577/ffa18.png)
Применяем операцию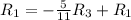 
к для того, чтобы сделать некоторые элементы строки равными 0.
![\left[\begin{array}{cccc}1&0&0&2 \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&1 &1 \end{array}\right]](/tpl/images/1055/0577/a5101.png)
Применяем операцию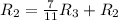 
к для того, чтобы сделать некоторые элементы равными 0.
![\left[\begin{array}{cccc}1&0&0&2\\0&1&0&-1\\0&0&1&1\end{array}\right]](/tpl/images/1055/0577/927aa.png)
Воспользуемся полученной матрицей для того, чтобы описать итоговое решение системы уравнений.
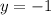
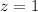
Решением является множество упорядоченных пар, которые удовлетворяют системе.
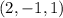
В сквере Губернаторского парка, недалеко от Круглой площади, возвышается памятник великому поэту, прозаику, государственному деятелю – Гавриилу Романовичу Державину. Высота монумента – 4,5 метра. Установлен в 2003 году, автор – скульптор из Финляндии Вальтер Сойни.
В Петрозаводске многое связано с именем Державина, и это не случайно. Гавриил Романович с 1784 по 1785 год был губернатором Олонецкой губернии, причем первым губернатором. Несмотря на краткость срока его пребывания на этом посту, он многое успел сделать для нового государственного образования (Олонецкая губерния была учреждена накануне его назначения). Новый губернатор организовал судебную, финансовую систему, открыл первую общегражданскую городскую больницу.
Петрозаводский период жизни нашел отражение в произведениях Державина-литератора. По результатам инспекционной поездки по губернии, была написана «Подённая записка …», одна из глав «Записок из известных всем происшествиев…» также посвящена этому времени. Есть и несколько стихотворений: «Водопад» (Пушкин считал его лучшим из поэтических произведений Державина), «Буря», «На счастие», «Ко второму соседу».
Жители города Петрозаводска чтут память своего знаменитого правителя и, накануне празднования 260-летия со дня его рождения, установили бронзовую фигуру губернатора в парадном мундире, высотой 2,7 м. на постаменте из красного гранита.