1. Пусть было х трехместных и у пятиместных лодок.
x+y = 7
В трехместные лодки поместилось 3x чел, а в пятиместные 5y чел. Всего в лодках был 31 турист.
3x+5y = 31
Составим и решим систему уравнений:
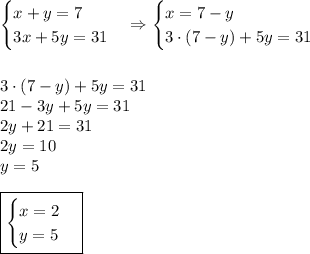 .
.
ответ: было 2 пятиместных и 5 трёхместных лодок.
2. Собственная скорость катера x км/ч, скорость течения реки y км/ч.
x+y км/ч скорость катера по течению
x-y км/ч скорость катера против течения
По течению 84 км проплыл за 3 часа:
(x+y)·3 = 84
Против течения 84 км проплыл за 3,5 часа:
(x-y)·3.5 = 84
Составим и решим систему уравнений:
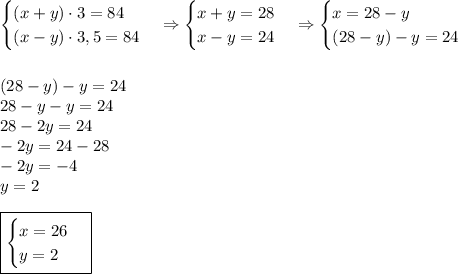
ответ: собственная скорость катера 26 км/ч, скорость течения реки 2км/ч.
1.Гоняют по кольцу. Длинна кольца 350 км. Старт и финиш в одной точке. Длинна этапа эстафеты - 75 км. Что ищем: наименьшее количество этапов. 2. А может 350 км разделится на 75 км, так что бы получилось число без остатка (что бы старт и финиш совпали) . Проверяем: 350:75=4,666... Нет не получилось. Тогда следующая точка совпадения будет - 2 круга, а это? 3. Два круга = 2 х 350км = 700 км. Может теперь разделится без остатка? Проверяем: 700:75=9,333... Нет, опять не получилось. Тогда следующая точка совпадения будет - 3 круга, а это? 4. Три круга = 3 х 350км = 1050 км. Снова ищем ровное число этапов. Проверяем: 1050:75=14. Свершилось! Ура!! ! ответ: наименьшее количество этапов 14(четырнадцать) , обоснованием ответа является решение-рассуждение.
Тогда, на основании данных задачи, составим следующую пропорцию: 2/75% так относятся к 14/25, как 100% относятся к Х.
Затем, на основании данной пропорции, составим следующее уравнение: Х х 2/75% = 14/25 х 100%.
Решая данное уравнение, получаем Х = (14 х 100 х 75) / (25 х 2) = 14 х 50 х 3 = 14 х 150 = 2100.
ответ: искомое число равно 2100
это из инета