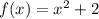Два охотника одновременно стреляют в цель. известно, что вероятность промаха у первого охотника равна 0,8, а у второго – 0,4. первый охотник стреляет в два раза чаще, чем второй охотник. найти вероятность того, что в результате случайно выбранного очередного выстрела одного из охотников будет допущен промах

👇

Увидеть ответ

Ответ:

JHOOOOOOPE

22.06.2020

вообще по теореме вероятности, но чтобы не заморачиваться

0,8*0,4=0,32

4,8(93 оценок)

Открыть все ответы

Ответ:

Kotik77789

22.06.2020

Пусть функция f(x)=x^2+2

определена на множестве E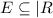 $E\subseteq |R$
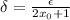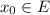Пусть $\delta=\frac{\epsilon}{2x_0+1}$ где $x_0 \in E$ .
Понятно, что для любого

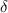на области $\delta$ от x_0

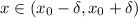(то есть: $x \in 
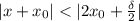(x_0-\delta,x_0+\delta)$ ) выполняется $|x+x_0|<|2x_0+ \frac{\delta}{2}|$ .
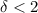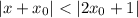Следовательно, для $\delta<2$ , выполняется |x+x_0|<|2x_0+1|

.

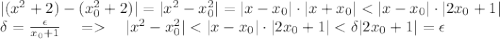
$|(x^2+2)-(x_0^2+2)|=|x^2-x_0^2|=|x-x_0|\cdot|x+x_0| < |x-x_0|\cdot|2x_0+1| \\
\delta= \frac{\epsilon}{x_0+1} \ \ \ = \ \ \ |x^2-x_0^2|< |x-x_0|\cdot|2x_0+1|<\delta|2x_0+1|=\epsilon$

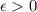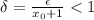Получили, что для любого $\epsilon 0$ есть $\delta=\frac{\epsilon}{x_0+1}<1$ , на области которой выполняется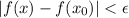 $|f(x)-f(x_0)|<\epsilon$
(Проще говоря:
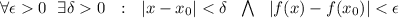$\forall
 \epsilon0 \ \ \exists\delta0 \ \ : \ \ |x-x_0|<\delta \ \ 
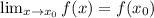\bigwedge \ \ |f(x)-f(x_0)|<\epsilon$ ). Следовательно - $\lim_{x 
\to x_0} f(x)=f(x_0)$ .
Что и требовалось доказать.
Для x_0=-1

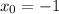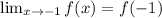нужно отдельно доказать предел $\lim_{x \to -1} f(x)=f(-1)$ .

Теперь в чём проблема самого вопроса: мы только что доказали непрерывность функции на любом подмножестве

. Но! Множество натуральных чисел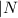

тоже подмножество

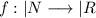, значит $f:|N \longrightarrow |R$ тоже непрерывна, получается - доказали что

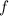непрерывна на области определения? Известно, что 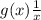$g(x) \frac{1}{x}$ тоже непрерывна на области определения, но

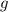, понятное дело, не определена на

!
Потому вопрос, ИМХО, поставлен не верно (претензия не к тебе, а скорее к преподавателям твоим). Правильно задать вопрос указывая то множесто точек, которое интересует: к примеру "непрерывна на

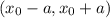" или, "непрерывна на отрезке (x_0-a,x_0+a)

"...
Тем более, что есть понятие "равномерная непрерывность" - свойство области, а не так, как "непрерывность" - свойство точки. Отсюда и непонимание.
А то получается: спрашивают об области, а проверяют точку.
Будут вопросы - пиши.

P.S. Исправил ошибки в наборе символов. Текста много :)

4,7(52 оценок)

Ответ:

kookie04

22.06.2020

Пусть сумма кредита равна S, а годовые составляют а %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент: b = 1 + 0,01a.
После первой выплаты сумма долга составит:
S1 = Sb − X.
После второй выплаты сумма долга составит:
S2 = S1b − X = (Sb − X)b − X = Sb² − (1 + b)X.
После третьей выплаты сумма оставшегося долга равна:
S3 = Sb³ - (1-b+b²)X = Sb³ -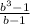 $\frac{b^{3} - 1}{b - 1}$ · X
После четвертой выплаты сумма оставшегося долга равна:
S4 = 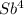$Sb^{4}$ - (1 + b +b² + b³)X = 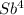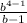$Sb^{4}$ - $\frac{ b^{4 - 1} }{b - 1}$ · X
По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому 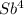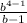$Sb^{4}$ - $\frac{ b^{4 - 1} }{b - 1}$ · X = 0.
Потом выражаешь из этого выражения X и при S = 6902000 и а = 12,5, получаем: b = 1,125 получается:
X = $\frac{6902000 * 1,601806640625 * 0,125 }{0,601806640625} = 2296350$ рублей