1. 80 + 25 = 105
80 + 30 = 110
80 + 65 = 145
80 + 80 = 160
2. 60 - 15 = 45
60 - 20 = 40
60 - 25 = 35
60 - 75 = -15
Пошаговое объяснение:
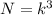 (1)
(1)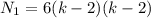 (2)
(2)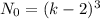 (3)
(3)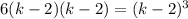 (4)
(4)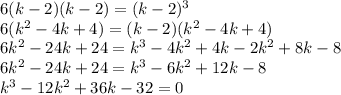
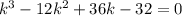 (5)
(5)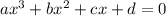
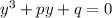
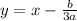
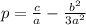
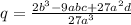
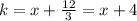 (6)
(6)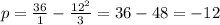
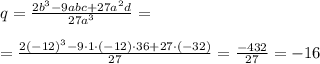
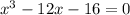 (7)
(7)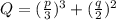
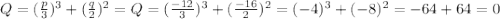
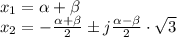
![\alpha = \sqrt[3]{ -\frac{q}{2} + \sqrt{Q} } \newline \newline \beta = \sqrt[3]{ -\frac{q}{2} - \sqrt{Q} }](/tpl/images/0410/1109/5992e.png)
![\alpha = \sqrt[3]{ -\frac{q}{2} + \sqrt{Q} } =\sqrt[3]{ \frac{16}{2} + \sqrt{0} }= \sqrt[3]{ 8}=2 \newline \newline \beta = \sqrt[3]{ -\frac{q}{2} - \sqrt{Q} }=\sqrt[3]{ \frac{16}{2} - \sqrt{0}}=\sqrt[3]{ 8}=2](/tpl/images/0410/1109/557a4.png)
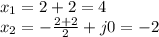 (8)
(8)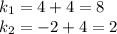 (9),
(9),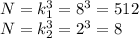 (10)
(10)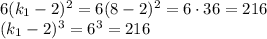 ок
ок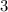 покраски ,
покраски , 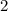 покраски , и одну это угловые реберные и серединные кубики.
покраски , и одну это угловые реберные и серединные кубики. 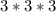 , и покрасить его две грани , тогда остается , 12 не покрашенных кубиков , то есть
, и покрасить его две грани , тогда остается , 12 не покрашенных кубиков , то есть 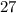
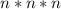 то центральных будет
то центральных будет 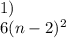 , а те внутри кубика
, а те внутри кубика 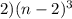
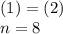
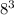 кубиков
кубиков
ответ:105, 110, 145, 160.
2) 45, 40, 35, -15
Пошаговое объяснение: