если ошибся жираф, то и мартышка ошиблась. Значит, ошибоась мартышка. Слону модет быть только 11 лет. ответ: 3
В) 5 минут
Пошаговое объяснение:
Дано:
V катера - 1 км за 2 мин = 500 м/мин
V лодки - в 5 раз больше T катера
Расстояние между ними - 3 км = 3 000 м
Найти:
Через сколько они встретятся - ? мин
1) 1 · 5 = 5 (мин) - Столько времени тратит лодка на 500 м.
2) 500 : 5 = 100 (м/мин) - V лодки
3) 100 + 500 = 600 (м/мин) - V сближения
T = S : V (T - время, S - расстояние, V - скорость
4) 3 000 : 600 = 5 (мин) - T через которое они встретятся
Теперь посмотрим варианты ответов:
А) 2 мин
Б) 3 мин
В) 5 мин
Г) 6 мин
В) 5 минут
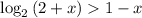 ;
;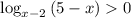 ;
; – строго монотонно возрастает ;
– строго монотонно возрастает ;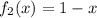 – строго монотонно убывает ;
– строго монотонно убывает ;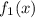 и
и 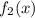 – единственно.
– единственно.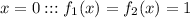 – это и есть пересечение, после которого монотонно возрастающая функция строго превышает убыващую, что и требуется в уловии (I).
– это и есть пересечение, после которого монотонно возрастающая функция строго превышает убыващую, что и требуется в уловии (I).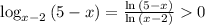 ;
;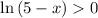 при
при 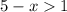 , а значит x < 4 ;
, а значит x < 4 ;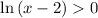 при
при 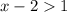 , а значит x > 3 ;
, а значит x > 3 ;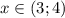 .
.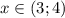 .
.