скорость время расстояние участок
пешком х км/ч 2 ч 2х км AB
на катере 2х км/ч 3 ч 2х*3=6 км BC
на автобусе 4*2х=8х км/ч 3 ч 8х*3=24 км CD
Итого: - 8 ч 160 км AD
Составим уравнение:
2х+6х+24х=160
32х=160
х=160:32
х=5 (км/ч) - пешая скорость туриста (на участке АВ)
2х=2*5=10 (км/ч) - скорость катера (на участке ВС)
8х=8*5=40 (км/ч) - скорость автобуса (на участке CD)
Найдём среднюю скорость туриста на всём участке пути:
v(ср.) = общее расстояние: общее время
160:(2+3+3)= 160:8=20 (км/ч) - средняя скорость движения
на участке от А до D
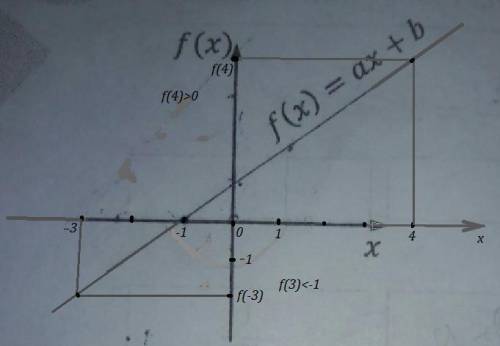
ответ: f(4)>0 ; f(-3)<-1 .
Пошаговое объяснение:
На чертеже всегда отмечается единичный отрезок (длина этого отрезка равна 1) . Отмечена точка пересечения с осью ОХ . Если считать отрезок от начала координат до этой точки единичным, то координаты точки пересечения прямой с осью ОХ (-1,0) .
Находим точки на оси ОХ с абсциссами х=4 и х= -3 . Проводим перпендикуляры от этих точек до пересечения с прямой. А от полученных точек на прямой проводим перпендикуляры к оси ОУ. Ординаты точек пересечения этих перпендикуляров с осью ОУ и будут значениями f(4) и f(-3) .
Сравниваем, выше или ниже нуля находится значение f(4) . В нашем случае f(4) выше 0, поэтому f(4)>0 .
Теперь сравниваем, выше или ниже числа (-1) находится значение f(-3) . В нашем случае f(-3) расположено ниже числа (-1), поэтому f(-3)<-1 .
ответ: 40,8 т
Пошаговое объяснение:
Задача на одинаковую продуктивность - скорость работы.
17 т : 5 ч = Х т : 12 ч - скорость работы - 3,4 т/ч
5*Х = 17*12 = 204
Х = 204 : 5 = 40,8 т за 12 ч