Question

Решить матрицу 2х-у-3=-9 х-5у+z=20 3х+4у+2z=15

Answer 1

Там несколько решения, надеюсь этот подойдет

Answer 2

$x_{1}$ ≈ -3.76

$x_{2}$ ≈ -1.52

$x_{3}$ ≈ 16.17

Пошаговое объяснение:

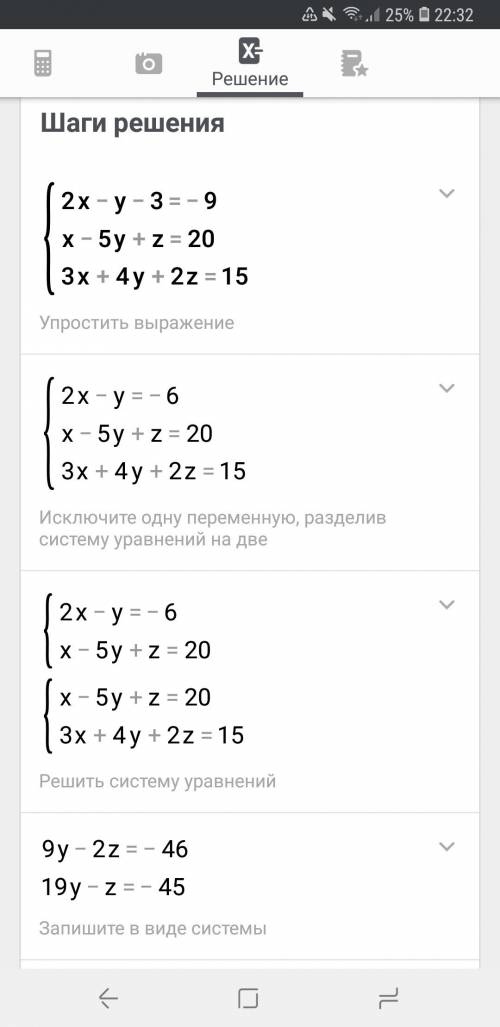
в первом уравнении -3 переносим вправо и получаем 2x-y=-6. Остальные уравнения не меняются.

Составляем матрицу неизвестных и находим ее детерминант:

D = $\left[\begin{array}{ccc}2&-1&0\\1&-5&1\\3&4&2\end{array}\right]$ = (2*(-5)*2) + ((-1) * 1 * 3) + (1 * 4 * 0) - (0 * (-5) * 3) - ((-1) * 1 * 2) - (2 * 4 * 1) = -20 - 3 + 2 - 8 = -29. D ≠ 0, значит существует 1 решение данной системы.

Составляем матрицу свободных членов:

$\left[\begin{array}{ccc}-6\\20\\15\end{array}\right]$

Теперь нужно найти 3 детерминанта (для каждой неизвестной).

Нужно взять матрицу D и заменить каждый столбец на матрицу свободных членов (сначала только первый, потом только второй и т.д.)

$D_{1}$ = $\left[\begin{array}{ccc}-6&-1&0\\20&-5&1\\15&4&2\end{array}\right]$ = 60 + 0 + 15 - 0 + 40 + 24 = 109

$D_{2}$ = $\left[\begin{array}{ccc}2&-6&0\\1&20&1\\3&15&2\end{array}\right]$ = 80 + 0 - 18 - 0 - 30 + 12 = 44

$D_{3}$$\left[\begin{array}{ccc}2&-1&-6\\1&-5&20\\3&4&15\end{array}\right]$ = -150 - 24 - 60 - 90 - 160 + 15 = -469

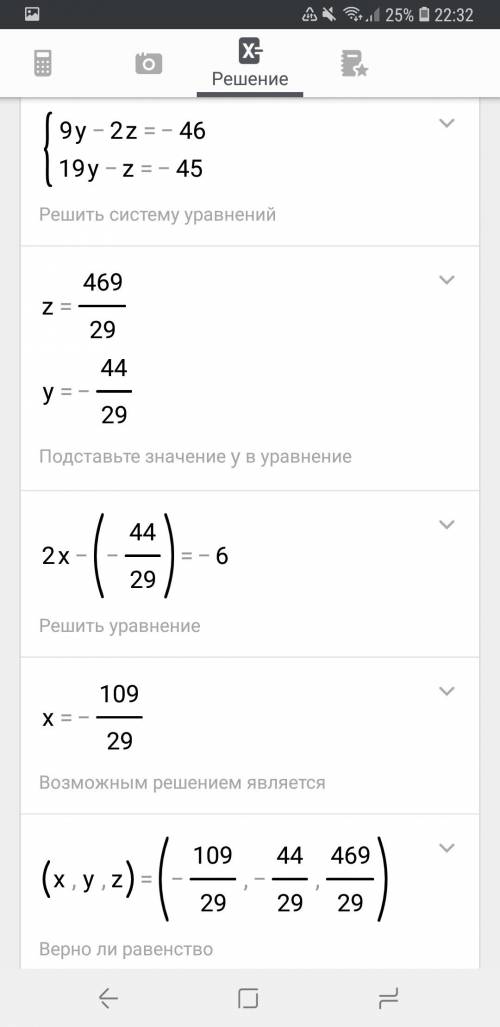
Теперь нужно взять $D_{1} , D_{2}, D_{3}$ и разделить их на главны детерминант (29).

$x_{1}$ = $\frac{109}{-29}$ ≈ -3.76

$x_{2}$ = $\frac{44}{-29}$ ≈ -1.52

$x_{3}$ = $\frac{-469}{-29}$ ≈ 16.17

Можно сделать проверку

2 * (-3.76) + 1.52 = -6

-3.76 - 5 * (-1.52) + 16.17 ≈ 20.01

3 * (-.76) + 4 * (-1.52) + 2 * (16.17) ≈ 14.98