Добрый день! С удовольствием помогу тебе решить эту задачу и объясню каждый шаг.
Итак, у нас есть два числа, и мы знаем, что отношение между ними равно 0,5:0,3. Чтобы решить эту задачу, нам нужно сначала найти сами числа.
Чтобы найти первое число, мы можем взять отношение и умножить его на второе число:
0,5/0,3 = 5/3
Теперь у нас есть отношение первого числа ко второму числу, и оно равно 5/3.
Мы также знаем, что разность этих двух чисел равна 1⅓. Чтобы найти разность, мы вычитаем второе число из первого числа:
(5/3) - (2/3) = 3/3
Таким образом, разность между двумя числами равна 3/3, что равно 1.
Теперь мы знаем, что первое число - второе число = 1. Так как мы уже нашли первое число в предыдущем шаге (5/3), мы можем решить уравнение:
(5/3) - второе число = 1
Чтобы найти второе число, вычтем 1 из 5/3:
(5/3) - 1 = (5/3) - (3/3) = 2/3
Таким образом, второе число равно 2/3.
Теперь у нас есть оба числа: первое число равно 5/3, а второе число равно 2/3.
Для того чтобы найти среднее арифметическое этих двух чисел, мы должны сложить их и разделить полученную сумму на 2:
(5/3 + 2/3) / 2 = (7/3) / 2
Чтобы делить дробь на число, мы можем умножить ее на обратное число:
(7/3) / 2 = (7/3) * (1/2) = 7/6
Таким образом, среднее арифметическое этих двух чисел равно 7/6.
Надеюсь, что моё объяснение понятно и помогло тебе выполнить задание. Если у тебя есть еще вопросы, не стесняйся задавать их!
Давай разберемся с этим математическим выражением. Мы должны упростить дробь (sin2x)/(20(cos^2x−sin^2x)). Для этого воспользуемся знаниями о тригонометрических тождествах.
1. Начнем с разложения sin 2x:
sin 2x = 2sin x cos x.
2. Заменим sin 2x на 2sin x cos x в исходной дроби:
(2sin x cos x)/(20(cos^2x−sin^2x)).
3. Раскроем скобки в знаменателе:
(2sin x cos x)/(20(cos^2x − sin^2x)) = (2sin x cos x)/(20cos^2x − 20sin^2x).
4. Мы можем разложить числитель и знаменатель на множители:
(2sin x cos x)/(20cos^2x − 20sin^2x) = (2sin x cos x)/(20cos^2x − 20(1 − cos^2x)).
5. Упростим выражение в знаменателе:
(2sin x cos x)/(20cos^2x − 20(1 − cos^2x)) = (2sin x cos x)/(20cos^2x − 20 + 20cos^2x).
6. Приведем подобные слагаемые в знаменателе:
(2sin x cos x)/(20cos^2x − 20 + 20cos^2x) = (2sin x cos x)/(40cos^2x − 20).
7. Заменим cos^2x на (1 − sin^2x):
(2sin x cos x)/(40cos^2x − 20) = (2sin x cos x)/(40(1 − sin^2x) − 20).
8. Упростим числитель и знаменатель:
(2sin x cos x)/(40(1 − sin^2x) − 20) = (2sin x cos x)/(40 − 40sin^2x − 20).
9. Поделим числитель и знаменатель на 2 для упрощения:
(2sin x cos x)/(40 − 40sin^2x − 20) = sin x cos x/(20 − 20sin^2x − 10).
10. Распишем знаменатель:
sin x cos x/(20 − 20sin^2x − 10) = sin x cos x/(-20sin^2x + 10).
Таким образом, упрощенный вид исходной дроби будет sin x cos x/(-20sin^2x + 10).
25b*(a+c)
-2cm*(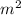 + 5cm - 13c)
+ 5cm - 13c)
-6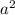 d * (3d - a) * (5d + a)
d * (3d - a) * (5d + a)
Пошаговое объяснение: