Найдем сначала общее решение соответствующего однородного дифференциального уравнения
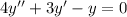
Пусть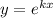 
, мы получим характеристическое уравнение
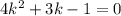
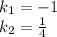
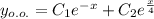— общее решение однородного диф. ур.
Найдём теперь частное решение. Рассмотрим функцию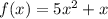 
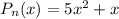отсюда 
; 
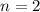. Сравнивая 
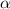с корнями характеристического уравнения и, принимая во внимая, что , частное решение будем искать в виде:
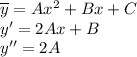
Подставляем в исходное дифференциальное уравнение
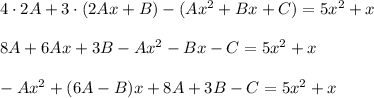
Приравниваем коэффициенты при степени x
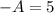откуда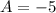 
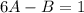откуда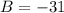 
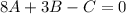откуда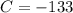 
Частное решение: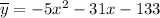 
Общее решение линейного неоднородного дифференциального уравнения:
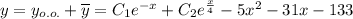
Найдем сначала общее решение соответствующего однородного дифференциального уравнения
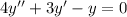
Пусть 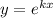, мы получим характеристическое уравнение
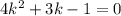
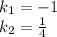
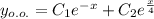— общее решение однородного диф. ур.
Найдём теперь частное решение. Рассмотрим функцию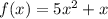
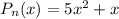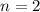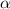отсюда ; . Сравнивая с корнями характеристического уравнения и, принимая во внимая, что , частное решение будем искать в виде:
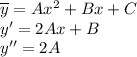
Подставляем в исходное дифференциальное уравнение
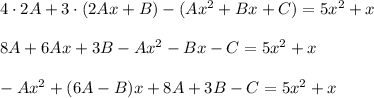
Приравниваем коэффициенты при степени x
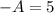откуда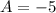
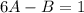откуда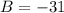
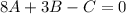откуда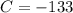
Частное решение: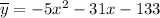
Общее решение линейного неоднородного дифференциального уравнения:
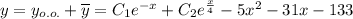
07:00 утра. На улице ещё темно, как в ночи. В 10-этажном доме не слишком обширного двора спал горожанин. Звон будильника в его комнате развеял напрягающую тишину. Человек встал, пытаясь не потревожить спящую рядом супругу. Он поспешил на кухню, чтоб перекусить перед сборами и работой. Когда завтрак был окончен, горожанин оделся, выключил свет и вышел из дома.
Он сел в машину и поехал на работу. Нудное времяпровождение на работе даже описывать не стоит. Это было бы слишком неинтересно. Человек вышел из большого здания, открыл машину, сел и уехал. По прибытию домой, он обнаружил, что его жена, кажется, в очередной раз ушла к подруге, оставив еду на столе. Горожанин вздохнул, разделся и сел смотреть телевизор. Через небольшое количество времени, супруга вернулась. Горожанин и его жена совершили водные процедуры и легли спать.
Конец.