6) приравниваем выражение под модулем к нулю. x=3/4
Нарисуем интервал и разобьём его на 2 отрезка: (-беск. до 3/4] и (3/4 до +беск.)
Берём из первого интервала любое число, например -100. Подставляем в выражение 4x-3. Получается отрицательное число, значит знак на интервале (-беск. до 3/4] "-".
Аналогично, для второго интервала, берём число 100, подставляем. Знак интервала (3/4 до +беск.) "+".
Раскрываем модуль на 1-ом интервале:
-7/3(4x-3)+7,2=9
x= 39/70
Проверяем на интервале (-беск. до 3/4]
Данное число входит в этот интервал, значит является корнем.
Также на 2-ом, со знаком "+".
7/3(4x-3)+7,2=9
x=33/35
Проверяем на интервале (3/4 до +беск.). Данный корень является решением
ответ: x=39/70, x2=33/35
1) х = 16
2) х = 12
3) z = 3
4) х = 14
Пошаговое объяснение:
1) x/4 = 36/9 правую часть можно сократить
х/4 = 4 домножаем пример на знаменатель(4)
х = 16
2) 1/6 = 2/х отсюда х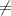
0(делить на 0 нельзя, а в примере мы делим на х), просто умножаем крестиком(1*х=2*6)
1х=12, х = 12
3) 5/z = 25/15 правую часть можно сократить z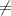0
5/z = 5/3 тут всё просто, 5делить на какое-то число = 5 делить на 3, очевидно что отсюда какое-то число(z) = 3
4) 7/4 = х/8, тут мы ничего не можем такого сделать, поэтому просто умножаем крестиком(или можно ещё домножить обе части на 8, выйдет что слева придётся умножить на два, а справа останется х, 14=х)
7*8=х*4
4х = 56
х = 14
a - (b - (c - (a - b))) + ( - c - ( a - (a + c ))) - c=0
a-(b-(c-a+b))+(-c-(a-a-c))-c=0 (а и -а сокращаем)
a-(b-c+a-b)+(-c+c)-c=0 (b и -b, а также с и -с сокращаем)
a+c-a-c=0 (а и -а, а также c и -c сокращаем)
Пошаговое объяснение: