Математическое ожидание - сумма попарных произведений значений случайной величины на вероятности, с которыми эти величины достигаются.
То есть, если значение 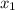 достигается с вероятностью
достигается с вероятностью 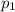 , значение
, значение  - с вероятностью
- с вероятностью  , и так далее, значение
, и так далее, значение 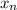 - с вероятностью
- с вероятностью 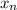 , то математическое ожидание:
, то математическое ожидание:
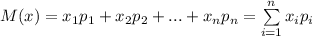
Математическое ожидание показывает среднее или наиболее вероятное значение случайной величины. В единичном испытании математическое ожидание равно вероятности события.
Для вычисления мат.ожидания как ожидаемого числа вопросов используем формулу:
 , где
, где  - вероятность осуществления некоторого события,
- вероятность осуществления некоторого события, 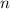 - число повторений.
- число повторений.
В нашем случае,  - вероятность того, что очередной вопрос не из группы "спринт",
- вероятность того, что очередной вопрос не из группы "спринт", 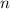 - число вопросов группы "спринт" (нас интересует сколько раз среди них встретится вопрос не группы "спринт").
- число вопросов группы "спринт" (нас интересует сколько раз среди них встретится вопрос не группы "спринт").
Поскольку вопросов не из группы "спринт" 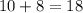 , а общее число вопросов
, а общее число вопросов  , то вероятность того, что очередной вопрос не из группы "спринт" равна:
, то вероятность того, что очередной вопрос не из группы "спринт" равна:

Число вопросов группы "спринт": 
Тогда:

Конечно, можно действовать по первой формуле.
Для этого рассмотрим возможные количества вопросов не из группы "спринт", которые могли оказаться в группе "спринт". Это количества: 0, 1, 2, ..., 17, 18.
Найдем вероятности осуществления этих возможностей. Так как общий смысл сохраняется во всех ситуациях, то рассмотрим нахождение вероятности в общем виде - найдем с какой вероятностью i вопросов не из группы "спринт" попадут в группу "спринт".
Число выбрать вопросы в группу "спринт" с учетом этого условия соответствует тому, что из 18 вопросов не группы "спринт" мы выберем некоторые i штук, а остальные (30-i) штук мы выберем из 30 вопросов группы "спринт". Итоговое число благоприятных комбинаций: 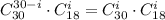 .
.
Общее число выбрать вопросы в группу "спринт" соответствует тому, что из всех 48 вопросов мы выберем некоторые 30 штук. Общее число комбинаций:  .
.
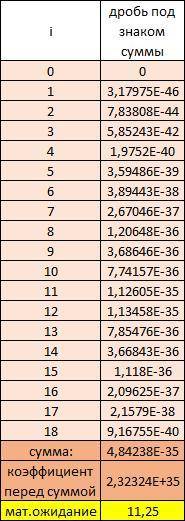
Тогда, ситуации, что в группе "спринт" окажется i вопросов не из группы "спринт", соответствует вероятность 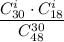 .
.
Запишем математическое ожидание как сумму попарных произведений значений на вероятность:

Можно попробовать упростить эту формулу:
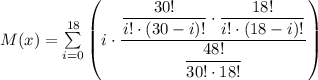

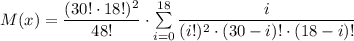
Далее нужно каким-либо досчитать эту величину. Вычисления дают полученный ранее результат:
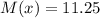
Учитывая контекст вопроса, а именно, что мат.ожидание соответствует числу вопросов, попавших в группу "спринт", запишем также округленное до целого числа значение мат.ожидания:
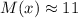
ответ: 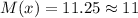
Пошаговое объяснение:
в первый день набрал 3а/5
во второй 1а/4
за два дня набрал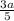 +
+ 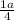
=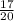 a
a
осталось набрать а -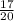 a =
a =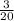 а
а