#6. 1-день - 200 км; 2-день - 175 км.
#8. 1 самолет пролетел - 3200 км;
2-ой самолет пролетел - 4800 км.
Пошаговое объяснение:
#6. По условию теплоход за 2 дня км.
В 1 день он был в пути 8 часов, а во 2 день - 7 часов.
Пусть скорость теплохода - х км/час.
Пройденное расстояние за 2 дня со скоростью х км/час - (8+7)*х
Уравнение:
(8+7)*х=375
15х=375
х=375:15
х=25 (км/час - скорость теплохода)
25*8=200 (км - пройдено в 1-день)
25*7=175 (км - пройдено во 2-день)
Проверка:
200+175=375
375=375
#8. Один самолет был в воздухе 4 часа, а другой - 6 часов и пролетел на 1600 км больше, чем первый.
Пусть скорость самолета - х км/час.
1-ый за 4 ч пролетел - 4х км, а
2-ой за 6 ч - 6х км.
Уравнение:
6х-4х=1600
2х=1600
х=1600:2
х=800 (км/час - скорость самолета)
800*4=3200 ( км - пролетел 1-ый)
800*6=4800 (км - пролетел 2-ой)
Проверка:
4800-3200=1600
1600=1600
Заметим, что основание логарифма 
меньше единицы. Это означает, чтобы значение самого логарифма было больше ноля (как требуется в неравенстве), нужно, чтобы его подлогарифмическое выражение было тоже меньше единицы (и больше ноля, в силу области определения логарифмических выражений):
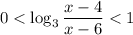
Все это можно довести до метода интервалов:
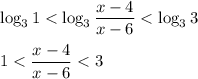
Первое неравенство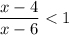 
можно решить так:
- - - + + +
__________
__________ 
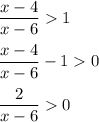
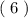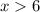
Второе неравенство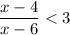 
решается схожим образом:
- - - + + + - - -
__________________
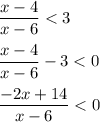
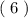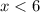_________ Или 
, или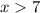 
.
Как пересечение решений двух неравенств имеем решение .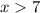
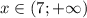
Значит, наименьшее целое число, удовлетворяющее неравенству - это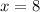 
, что сходится с ответом.
2)145:5 + 455:5 = 29 + 91 = 120;
3)6324:102 + 14076:102 = 62 + 138 = 200.