Пошаговое объяснение:
1) Координаты середины отрезка - это среднее арифметическое от координат концов отрезка.
C( (-3+5)/2 ; (-4-2)/2 ) = (2/2; -6/2) = (1; -3)
2) Радиус окружности - это расстояние между ее центром и точкой B.
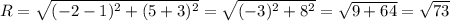
Уравнение окружности
(x-x0)^2 + (y-y0)^2 = R^2, где (x0; y0) - координаты точки О.
(x-1)^2 + (y+3)^2 = 73
3) Точка М сдвинута от точки N на такое же расстояние и в том же направлении, как точка F от точки К.
F(K-2; K-1) = (8-2; -1-1) = (6; -2)
M(N-2; N-1) = (5-2; 5-1) = (3; 4)
ответ: M(3; 4)
4) Уравнение прямой по двум точкам
(x - x1)/(x2 - x1) = (y - y1)/(y2 - y1)
(x + 3)/(2 + 3) = (y - 15)/(-1 - 15)
(x + 3)/5 = -(y - 15)/16
Это каноническое уравнение.
Можно преобразовать в общий вид ax + by + c = 0
16(x + 3) = -5(y - 15)
16x + 48 = -5y + 75
16x + 5y - 27 = 0
Или в вид с угловым коэффициентом y = kx + b
5y = -16x + 27
y = -16x/5 + 27/5
5) Нужно найти точку на оси ординат, то есть x = 0, которая лежит на одинаковом расстоянии от точек М и N. Это точка А(0; y)
|AM| = |AN|
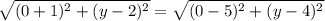
Избавляемся от корней и раскрываем скобки
1 + y^2 - 4y + 4 = 25 + y^2 - 8y + 16
Приводим подобные
8y - 4y = 36
y = 36/4 = 9
ответ: (0; 9)
6) Если прямые параллельны, то коэффициенты при х одинаковы.
Уравнение имеет вид: y = 7x + b
Теперь окружность. Приведем уравнение к обычному виду.
x^2 + y^2 - 10x - 2y + 20 = 0
(x^2 - 10x + 25) - 25 + (y^2 - 2y + 1) - 1 + 20 = 0
(x - 5)^2 + (y - 1)^2 = 6
Центр этой окружности O(5; 1)
Уравнение прямой (x - 5)/1 = (y - 1)/7
7(x - 5) = y - 1
y = 7x - 35 + 1
ответ: y = 7x - 34
Пошаговое объяснение:
1) Координаты середины отрезка - это среднее арифметическое от координат концов отрезка.
C( (-3+5)/2 ; (-4-2)/2 ) = (2/2; -6/2) = (1; -3)
2) Радиус окружности - это расстояние между ее центром и точкой B.
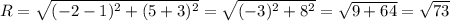
Уравнение окружности
(x-x0)^2 + (y-y0)^2 = R^2, где (x0; y0) - координаты точки О.
(x-1)^2 + (y+3)^2 = 73
3) Точка М сдвинута от точки N на такое же расстояние и в том же направлении, как точка F от точки К.
F(K-2; K-1) = (8-2; -1-1) = (6; -2)
M(N-2; N-1) = (5-2; 5-1) = (3; 4)
ответ: M(3; 4)
4) Уравнение прямой по двум точкам
(x - x1)/(x2 - x1) = (y - y1)/(y2 - y1)
(x + 3)/(2 + 3) = (y - 15)/(-1 - 15)
(x + 3)/5 = -(y - 15)/16
Это каноническое уравнение.
Можно преобразовать в общий вид ax + by + c = 0
16(x + 3) = -5(y - 15)
16x + 48 = -5y + 75
16x + 5y - 27 = 0
Или в вид с угловым коэффициентом y = kx + b
5y = -16x + 27
y = -16x/5 + 27/5
5) Нужно найти точку на оси ординат, то есть x = 0, которая лежит на одинаковом расстоянии от точек М и N. Это точка А(0; y)
|AM| = |AN|
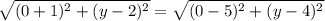
Избавляемся от корней и раскрываем скобки
1 + y^2 - 4y + 4 = 25 + y^2 - 8y + 16
Приводим подобные
8y - 4y = 36
y = 36/4 = 9
ответ: (0; 9)
6) Если прямые параллельны, то коэффициенты при х одинаковы.
Уравнение имеет вид: y = 7x + b
Теперь окружность. Приведем уравнение к обычному виду.
x^2 + y^2 - 10x - 2y + 20 = 0
(x^2 - 10x + 25) - 25 + (y^2 - 2y + 1) - 1 + 20 = 0
(x - 5)^2 + (y - 1)^2 = 6
Центр этой окружности O(5; 1)
Уравнение прямой (x - 5)/1 = (y - 1)/7
7(x - 5) = y - 1
y = 7x - 35 + 1
ответ: y = 7x - 34
В течение всей жизни Шишкин писал лес. «Но самой мощной по своему звучанию явилась картина «Афонасовская корабельная роща близ Елабуги» (. Прозрачный ручей на переднем плане, в котором можно сосчитать все камушки. На опушке изображен сосняк - стройный, высокий. Каждое дерево обладает своим «характером». В произведении воплощено то глубокое знание природы, которое было накоплено мастером за почти полувековой творческий путь. Монументальная картина (самая крупная по размеру в творчестве Шишкина) - последний торжественный образ леса в созданной им эпопее, символизирующей богатырскую силу русской природы.
Эта картина - художественное завещание мастера, торжественный финал той эпопеи леса, что он увлеченно писал на протяжении всей своей жизни. Она - свидетельствуя о том, что и в старости художник нисколько не утерял твердости руки, зоркости взгляда к типизации при сохранении точности фактуры и деталировки, - словно суммирует все достоинства шишкинской творческой манеры. Пейзаж представляет зрителю высший летний расцвет. Шишкин вообще любил высшие точки состояний природы, равно как и наиболее мощные и стойкие породы деревьев.
Картина «Утро в сосновом лесу» пользуется популярностью занимательным сюжетом. Однако истинной ценностью произведения является прекрасно выраженное состояние природы. Показан не глухой дремучий лес, а солнечный свет, пробивающийся сквозь колонны великанов, чувствуется глубина оврагов, мощь вековых деревьев. И солнечный свет как бы робко заглядывает в этот дремучий лес. Чувствуют приближение утра резвящиеся медвежата. «Замысел картины подсказал Шишкину Савицкий К.А.. Медведей написал Савицкий в самой картине. Эти медведи с некоторыми различиями в позах и количестве (сначала их было двое) фигурируют в подготовительных рисунках и эскизах» (с.40,1). Медведи получились у Савицкого столь удачно, что он даже расписался на картине вместе с Шишкиным. А когда эту картину приобрел Третьяков, он снял подпись Савицкого, оставив авторство за Шишкиным.
О графическом мастерстве Шишкина можно судить по рисунку "Дубки под Сестрорецком" (1857). Наряду с присущими этой большой "рисованной картине" элементами внешней романтизации образа, в ней есть и ощущение натурности изображения. В произведении видно стремление художника к пластической трактовке природных форм, хорошая профессиональная выучка.
Уже один из ранних картин Шишкина «Ручей в лесу» (1870) свидетельствует о прочности профессионального фундамента гравера, за которым стоит творческая работа. Многодельный, сложный по мотиву, эта картина напоминает те рисунки пером и тушью, которые Шишкин исполнял в шестидесятые годы. «Но по сравнению с ними, при всей измельченности штрихов, он лишен какой-либо засушенности, в нем больше чувствуется красота чеканных линий, богаче светотеневые контрасты.
Картина «В лесу графини Мордвиновой» поражает нас не свойственной Шишкину проникновенностью и сосредоточенностью настроения. На картине солнце почти не попадает из-за густого леса, из-за чего деревья выглядят чахлыми. «И вот среди этого лесного царства вдруг возникает фигура старика-лесника, сразу незаметного – его одежда по цвету сродни лесу» ). Есть в этом пейзаже особенная поэтичность и даже таинственность. Совсем другая по настроению картина «Дождь в дубовом лесу». Здесь исчезла всякая таинственность. Лес выглядит небольшим и просторным. Идущие под дождем люди усиливают ощущение обжитости природы.
Шишкин любил также рисовать просторы. Один из таких пейзажей - «Лесные дали». Лес на данной картине отступил от переднего плана. Тонкая сосна, четко рисующаяся на фоне светлого неба, как бы отмеряет расстояние, а дальше уже начинаются леса. Вдалеке виднеется река или озеро. А за ней опять гряды лесов. «Небо золотистое, бесконечное. Тишина… Завораживающий простор. Туманная дымка постепенно заволакивает дали…»
Шишкин написал множество прекрасных картин, в которых отразил всю свою любовь и великолепие природы.