Лена ответила на 11 вопросов викторины, больше всех
Катя ответила на 8 вопросов викторины, меньше всех
Две другие одноклассницы могли ответить на 9 или 10 вопросов.
На каждый вопрос правильный ответ дали 3 одноклассницы, то есть количество всех верных ответов по всем вопросам викторины кратно трём.
Количество вопросов викторины можно посчитать так :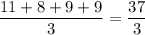
- не подходит, 37 не кратно 3
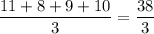- не подходит, 38 не кратно 3
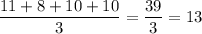
ответ : в викторине было 13 вопросов. Лена ответила на 11 вопросов, Катя на 8 вопросов, а две другие одноклассницы ответили на 10 вопросов каждая.
Даны точки P(-1,2,1); Q(3 ,-4 , 2) и плоскость 2x + 4y - 3z + 5=0.
Находим координаты вектора m, проходящего через точки P и Q.
m = (3-(-1)=4; -4-2=-6; 2-1=1) = (4; -6; 1).
Второй вектор - это нормальный вектор заданной плоскости. Он будет лежать в искомой плоскости. Его координаты берём из уравнения:
n = (2; 4; -3).
Теперь берём точку P(-1,2,1) и 2 вектора, которые будут лежать в искомой плоскости: m = (4; -6; 1) и n = (2; 4; -3).
Плоскость, проходящая через точку М0(х0;у0;z0) и параллельная данным (непараллельным между собой) прямым K1 и K2 (или векторам a1 и а2), представляется уравнением:
x-x0 y-y0 z-z0
nx ny nz
mx my mz = 0.
Подставляем данные:
x+1 y-2 z-1
2 4 -3
4 -6 1 = 0.
Решив эту матрицу, получаем -14x - 14y - 14z + 42 = 0.
Сократив на -14, получаем уравнение искомой плоскости:
x + y + z - 3 = 0.
1)25-5=20
2)4+6=10
3)7+2=9
ответы:20;10;9