ответ: min y = -3, max y = -1.
Пошаговое объяснение:
Находим производную.
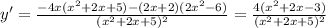
Приравниваем нулю множитель числителя с переменной.
Решаем уравнение x^2+2*x-3=0.
Ищем дискриминант:
D=2^2-4*1*(-3)=4-4*(-3)=4-(-4*3)=4-(-12)=4+12=16;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√16-2)/(2*1)=(4-2)/2=2/2=1;
x_2=(-√16-2)/(2*1)=(-4-2)/2=-6/2=-3.
Находим знаки производной в промежутках между критическими точками.
x = -4 -3 0 1 2
y' = -0,118343 0 0,48 0 -0,118343 .
Как видим, в точке х = -3 минимум функции, а в точке х = 1 - максимум.
Находим значения функции в этих точках.
у(-3) = (-2(9+3))/(9-6+5) = -24/8 = -3.
у(1) = (-2(1+3))/(1+2+5) = -8/8 = -1.
На заданном промежутке [-5; 1] значение функции у(1) = -1 является максимальным, а у(-3) =-3 минимальным.
Эстафета «Равновесие».
Напротив каждой команды стоят 2 гимнастические скамейки. На первой скамейке поставлены 3 кубика, на расстоянии 50 см друг от друга. По сигналу бежит первый участник, добежав до скамейки, идет по ней высоко поднимая ноги, перешагивает через кубики, стараясь не сбить их, затем пробегает по второй скамейке, обегает флажок и возвращается в свою команду, передав эстафету следующему участнику. Выигрывает команда, закончившая эстафету первой.
Эстафета «Лабиринт».
Напротив каждой команды установлены 5-6 скрепленных обручей. Впереди и в конце команды — старшеклассники. По сигналу все участники команды, взявшись за руки, бегут и пролезают змейкой сквозь обручи, обегают флажок и возвращаются па прежнее место. Выигрывает команда, закончившая эстафету первой.
Пока идет подсчет результатов, зрителям предлагаются показательные выступления по художественной гимнастике.
Эстафета с элементами акробатики.
Напротив каждой команды лежат 3 гимнастических мата на расстоянии одного метра друг от друга. По сигналу бежит первый участник каждой команды и выполняет лазанье на четвереньках на первом мате; на втором мате выполняет перекаты из исходного положения лежа на спине, руки вверх; на третьем мате выполняет кувырок вперед, обегает флажок и возвращается в.свою команду, передает эстафету второму участнику. Выигрывает команда, закончившая эстафету первой.
Эстафета «Переправа через ручей».
Шефы-старшеклассники удерживают гимнастическую палку на уровне груди. Первый участник выполняет вис. В таком положении шефы переносят всех своих учеников «на другой берег» — противоположную сторону площадки, где лежит длинная скакалка. Берут скакалку, вращают, дети пробегают и выстраиваются на первоначальное место.
Игровые эстафеты
Эстафета «Прыгуны и пятнашки».
Участники делятся на 2 команды, каждая из которых выстраивается вдоль боковых сторон зала лицом к середине. Одна команда — «Прыгуны», вторая — «Пятнашки» (бегуны); на площадке делается разметка. В 1 м от лицевой границы площадки проводится стартовая линия (для бегунов), а впереди, через 3 м, — вторая стартовая линия (для прыгунов). Перед этой линией (в 10-12 м от неё) чертят полосу шириной 1,5-2 м. По команде «На старт!» четыре прыгуна из команды «Прыгуны» занимают места за второй линией. За ними становятся бегуны. По команде «Внимание!» прыгуны и пятнашки принимают положение высокого старта, а по команде «Марш!» все выбегают вперед. Задача прыгунов — быстрее достичь полосы и перепрыгнуть через неё. Задача пятнашек — успеть осалить прыгунов. Если прыгуна не успевают осалить до прыжка, его команда получает очко. Пятнашка, который коснется прыгуна рукой до начала прыжка, получает очко.
Целые - 60% Дырявые - 40 % Сколько всего носков - ? . Решение : 1) 60-50= 10% 4 носка . 2) 100:10*4=40 носков было всего .
Пошаговое объяснение: