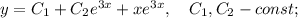
Пошаговое объяснение:
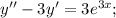
Это неоднородное уравнение. Сначала решим соответствующее ему однородное уравнение:
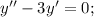
Составим и решим характеристическое уравнение:
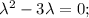
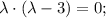

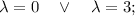
Имеем 2 различных действительных корня. Запишем общее решение однородного уравнения:
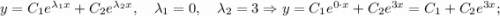
Вернёмся к неоднородному уравнению.
Показатель степени экспоненты содержит коэффициент, равный одному из корней характеристического уравнения, поэтому частное решение будем искать в виде
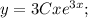
Найдём первую и вторую производные:
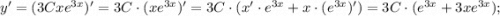
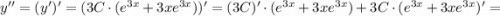
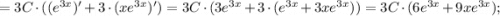
Подставим полученные производные в исходное уравнение:
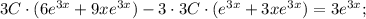
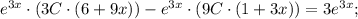
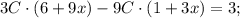
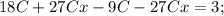
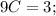
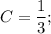
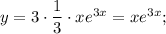
Проверим, верно ли найдено частное решение неоднородного уравнения. Воспользуемся ранее найденными производными:
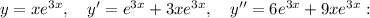
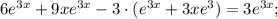
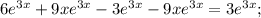
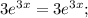
Частное решение найдено верно.
Общим решением неоднородного дифференциального уравнения является сумма общего решения однородного ДУ и частного решения неоднородного ДУ:
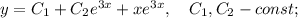
Пошаговое объяснение:
1) |х-1,5|=4
х-1,5=4
х₁=5,5
х-1,5=-4
х₂=-2,5
2) |3-х|=5
3-х=5
х=3-5
х₁=-2
3-х=-5
х=3+5
х₂=8
3) |2х-3|=0
2х-3=0
2х=3
х=3/2
х=1,5
4) |6-5х|=0
6-5х=0
5х=6
х=6/5
х=1,2
5) |х+1|+5=3
|x+1|=3-5
|x+1|=-2 модуль не может быть отрицательным
Решений нет.
6) |х+5|-2=7
|x+5|=7+2
|x+5|=9
x+5=9
x=9-5
x₁=4
x+5=-9
x=-9-5
x₂=-14
7) |10х+6|=4
10x+6=4
10x=4-6
10x=-2
x₁=-0.2
10x+6=-4
10x=-4-6
10x=-10
x₂=-1
8) |1/m|=1/4
1/m=1/4
m₁=4
1/m=-1/4
m₂=-4
9) |3х-9|=6
3x-9=6
3x=15
x=15/3
x₁=5
3x-9=-6
3x=3
x₂=1
10) |5/m|=2/3
5/m=2/3
m=5*3/2
m₁=7.5
5/m=-2/3
m=-5*3/2
m₂=-7.5
11) |2,4x+1,2|=6
2.4x+1.2=6
2.4x=4.8
x=4.8/2.4
x₁=2
2.4x+1.2=-6
2.4x=-7.2
x₂=-3
12) |1/2n|=1/4
1/2n=1/4
n=1/4*2
n₁=1/2
1/2n=-1/4
n=-1/4*2
n=-1/2
2)16
3)78
думаю правильно заранее