На столе стояло 100 на вид неотличимых коробок конфет, две из которых весили по два килограмма, а оставшиеся по одному килограмму. а ещё были чашечные весы, которые взвешивали правильно только тогда, когда на левой чашке был ровно один предмет, а на правой - ровно два. за рубль можно провести на весах одно взвешивание. удастся ли даше без посторонних предметов найти обе двухкилограммовые коробки конфет, если у неё есть ровно 101 рубль?

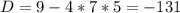 \
\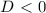 - это значит, что действительных решений уравнения нет.
- это значит, что действительных решений уравнения нет. 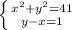
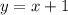
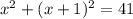
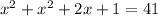
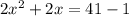
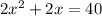
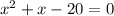
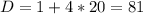
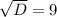
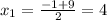
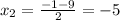
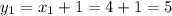
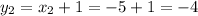
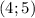 и
и 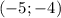
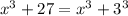
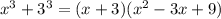 - разложили на множители.
- разложили на множители. 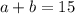
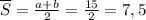
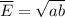
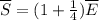
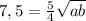
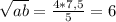
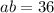
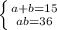
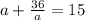
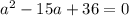
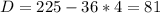
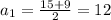
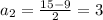
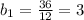
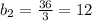
2. Задание
Выражаем y из второго:
Подставляем в 1 уравнение:
Теперь, зная значения х, находим значения y
ответ:
3 Задание.
Мы видим сумму кубов, раскладываем по формуле сокращенного умножения, получаем:
4 задание.
a и b - это числа, которые надо найти.
Их среднее арифметическое равно
Среднее геометрическое этих двух чисел равно:
По усовию среднее арифметическое больше на четверь ср.геометрического, то есть:
Возведём в квадрат:
Теперь у нас получилась такая простая система:
Решаем систему
Вот мы и нашли числа a = 12 и b = 3, или наоборот.