Любое число от 100 до 109
Пошаговое объяснение:
Обратим внимание, что при вычитании из числа суммы его цифр получаем число, которое делится на 9.
Пойдем с конца: покажем, что последнее число - эта цифра.
Пусть последнее число X и
,
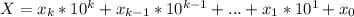здесь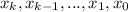 
- цифры числа X. По условию
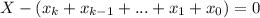или
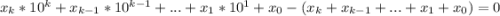
После раскрытия скобку и упрощения получим:
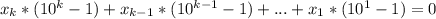
Но все числа в скобке положительные и поэтому сумма равна 0 тогда и только тогда, когда
.
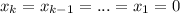Тогда X ≡ x₀, то есть цифра!
Каждый раз рассматривается разность некоторого числа и с суммой его цифр. Покажем что все разности делятся на 9. Пусть разность Y получено в некотором шаге и
.
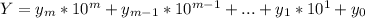Рассмотрев разность как выше получим:
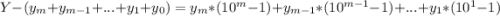
которое равносильно равенству
.
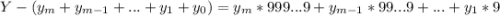Отсюда очевидно, что последняя сумма и в силу этого разность делится на 9. Отсюда, и числа получаемые на каждом шаге делятся на 9!
Так как из однозначных чисел делится на 9 только 9, то на 11-шаге рассматривается разность 9-9=0.
Следующее число при вычитании суммы его цифр должно давать 9, такое число 18 (10-шаг). Следующие числа:
27 (9-шаг); 36 (8-шаг); 45 (7-шаг); 54 (6-шаг); 63 (5-шаг); 72 (4-шаг); 81 (3-шаг).
Число 81 можно получить из числа 90 (90-(9+0)=81) или 99 (99-(9+9)=81).
Но число 90 нельзя получить таким Следовательно, следующее за числом 81 будет число 99 (2-шаг).
А число 99 можно получить из чисел от 100 до 109 (1-шаг: первое число).
18 карточек
Пошаговое объяснение:
Найдём количество чисел которые делятся на 2 с арифметической прогрессии.
Пусть a₁ = 10, aₙ = 48, d = 2 и нам необходимо найти n
Воспользуемся формулой: aₙ = a₁ + (n-1)·d
Выразим из этой формулы n:
Подставим известные данные и найдём n:
Значит в данном наборе содержится 20 чисел, которые делятся на 2
Количество чисел которые делятся на 7 в данном наборе не так много и их можно просто перечислить.
На 7 делятся числа 14, 21, 28, 35, 42 и 49 - всего 6 чисел.
Но числа 14, 28 и 42 мы уже учли, так как они делятся на 2.
Поэтому количество чисел, которые делятся на 2 или 7 равно:
20 + (6 - 3) = 20 + 3 = 23 числа
Следовательно, количество чисел, которые не делятся на 2 или 7 равно 40 - 23 = 17 чисел
Мы можем взять не глядя 17 карточек, но все числа на них могут не делиться на 2 или 7, но если мы возьмём ещё как минимум одну карточку, то мы найдём как минимум одно число, которое делится на 2 или 7.