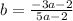
Свойства степеней(≈7 класс):
Упростите 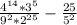
Квадратное уравнение(≈8 класс):
x² – 46x + 529 = 0
С использованием производной(≈11 класс):
y(x) = x⁴ + x³ - 5x² - x + 17
y'(2) = ?
↓↓↓↓↓
Свойства степеней(решение):
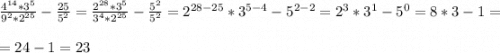
Квадратное уравнение(решение):
x² – 46x + 529 = 0
D = b² - 4ac = (-46)² - 4 * 1 * 529 = 2116 - 2116 = 0 => один корень
x = -b/2a = -(-46)/2 = 46/2 = 23
С использованием производной(решение):
y(x) = x⁴ + x³ - 5x² - x + 17
y'(2) = ?
y'(x) = (x⁴)' + (x³)' - (5x²)' - (x)' + (17)' = 4x³ + 3x² - 10x - 1
y'(2) = 4*2³ + 3*2² - 10*2 - 1 = 4*8 + 3*4 - 20 - 1 = 32 + 12 - 21 = 44 - 21 = 23
4 решения:
(sqrt(1,5);2,5+2*sqrt(1,5))
(-sqrt(1,5);2,5-2*sqrt(1,5))
(sqrt(0,5),1,5+2*sqrt(0,5))
(-sqrt(0,5),1,5-2*sqrt(0,5))
Пошаговое объяснение:
ОДЗ проверим получив решения.
Второе уравнение при выполнении ОДЗ
равносильно
у-4х=(2+2х-у)^2/y
y^2-4ху=(2+2х-у)^2
y^2-4ху=4+y^2+4x^2+8x-4y-4xy
0=4+4x^2+8x-4y
y=(x+1)^2
2x-y=2x-x^2-2x-1=-x^2-1
3^(2x-y)=(1/3) 3^(-x^2)
Обозначим 3^(х^2)=a
9/a+a=4*sqrt(3)
a^2-4*sqrt(3)*a+9=0
По теореме Виета а1=3*sqrt(3) а2=sqrt(3)
Значит х^2=1,5 или х^2=0,5
Пусть х=sqrt(1,5)
тогда у1=(1+sqrt(1,5)):2=2,5+2*sqrt(1,5)
По ОДЗ подходит 2,5-2*sqrt(1,5)>0
Если х=-sqrt(1,5), то
у=(1-sqrt(1,5))^2=2,5-2*sqrt(1,5) убеждаемся, что по ОДЗ подходит.
Пусть х=sqrt(0,5)
y=1,5+2*sqrt(0,5) по ОДЗ подходит
Пусть х=-sqrt(0,5)
у=1,5-2*sqrt(0,5) по ОДЗ подходит
Итак, 4 решения:
(sqrt(1,5);2,5+2*sqrt(1,5))
(-sqrt(1,5);2,5-2*sqrt(1,5))
(sqrt(0,5),1,5+2*sqrt(0,5))
(-sqrt(0,5),1,5-2*sqrt(0,5))