Радиус равен половине стороны куба.
8/2=4
ответ: 4
Для начала поработаем со вторым выражением. Первые три слагаемых свернем в квадрат разности: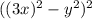 
; В следующих двух слагаемых вынесем общий множитель "40": 
; В итоге получим следующее уравнение: 
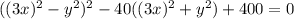. В скобках мы видим похожие выражения, отличающиеся лишь знаком посередине (такие выражение называются сопряженными). А хотелось бы видеть там равные (строго говоря тождественные) выражения. Пусть в первой скобке вместо 
будет стоять 
; Это приведет к тому, что придется убавить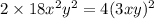 
; В итоге: 
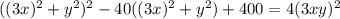; Слева стоит квадрат суммы. Уравнение примет вид: 
; Сворачивая еще раз: 
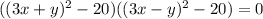; Получаем серию прямых: 
; А теперь приступим к рассмотрению первого уравнения.
Это уравнение задает круг с центром в точке (0, 0) и радиусом 
; Рассмотрим прямую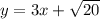 
; Найдем радиус окружности с центром в начале координат, которая касается данной прямой. Это легко сделать из подобия треугольников. 
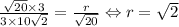; Значит, круг касается всех этих четырех прямых. Достаточно найти только координаты касания с любой из прямых. Это делается так же, как и находился радиус окружности. Для той же прямой это координаты 
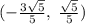; Ну а все решения:
прямые параллельны по 2 му признаку - равенству накрест лежащих углов ∠РЕМ = ∠1
Пошаговое объяснение:
2й признак параллельности прямых гласит
Если при пересечении двух прямых третьей секущей накрест лежащие углы равны, или соответственные углы равны, или сумма односторонних углов равна 180° — то прямые параллельны.
в нашем случае докажем, что накрест лежащие углы равны.
у нас накрест лежащие углы это ∠РЕМ и ∠1. докажем их равенство
РМ =РЕ , значит ΔРМЕ - равнобедренный, а значит ∠РЕМ = РМЕ
а поскольку по условию ∠РМЕ (∠2) =∠1, то ∠РЕМ = ∠1
что и требовалось доказать
4см
Пошаговое объяснение: