0
Пошаговое объяснение:
Первые 5 мест ряда чисел занимают однозначные нечётные числа. Всего их 5 и для их записи использовано 5 цифр (13579)
Затем, идут двузначные нечётные числа: 11,...,99. Всего их (99-9):2=45. Т.е. для их записи использовано 45*2=90 цифр.
Получаем уже 5+90=95 цифр.
Осталось ещё 5 цифр до ста цифр.
За числом 99 следуют трёхзначные нечётные числа 101 и 103, которые занимают 6 мест. Нас интересует цифра, стоящая на 5-ом месте. Это цифра ноль.
Итак, на сотом месте находится цифра ноль.
1. НОД(А,В) = 2²⁸*3²⁹
НОК(А,В) = 2⁶⁵*3⁷⁴*5²⁸
2. а) 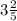 ; б)
; б) 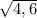
Пошаговое объяснение:
Задание 1.
А= 2³⁷*3¹⁵*12¹⁴ = 2³⁷*3¹⁵*(2²*3)¹⁴ = 2³⁷*3¹⁵*2²⁸*3¹⁴ = 2³⁷⁺²⁸ * 3¹⁵⁺¹⁴ = 2⁶⁵*3²⁹
В = 3⁷⁴ *10²⁸ = 3⁷⁴ *(2*5)²⁸ = 3⁷⁴*2²⁸*5²⁸
НОД(А,В) = 2²⁸*3²⁹
НОК(А,В) = 2⁶⁵*3⁷⁴*5²⁸
Задание 2.
a) x∈[√11; √13] и x∈Q (Q- множество рациональных чисел)
x=?
√11 ≈ 3,32 √13 ≈ 3,66
3,32 < x < 3,66
Например, x= 3,4 = 3 4/10 = 3 2/5 (∈Q)
x= 3,5 = 3 5/10 = 3 1/2 (∈Q)
x= 3,6 = 3 6/10 = 3 3/5 (∈Q)
(приведено сразу 3 примера такого рационального числа, на самом деле, их бесконечное множество).
б) x∈[2,1; 2,2], x∈I (I - множество иррациональных чисел)
2,1 = √(2,1)² = √4,41
2,2 = √(2,2)² = √4,84
√4,41 < x < √4,84
Например, х=√4,6 или х=√4,71 или х=√4,782 или х=√4,815
(приведено сразу 4 примера такого иррационального числа, на самом деле, их бесконечное множество).
1.Чтобы найти расстояние, нужно скоростьумножить на время.
2.Чтобы найти время, надо расстояние разделить на скорость.
3.Чтобы найти скорость, надо расстояние разделить на время.