
Пошаговое объяснение:
Для вычисления интеграла 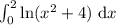 воспользуемся сначала методом интегрирования по частям:
воспользуемся сначала методом интегрирования по частям:
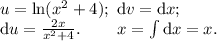
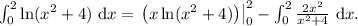
Заметим, что 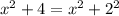 , и тогда в интеграле после интегрирования по частям напрашивается такая замена:
, и тогда в интеграле после интегрирования по частям напрашивается такая замена:
Если 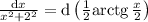 , то, положив
, то, положив 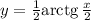 , найдём, что:
, найдём, что:
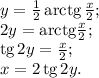
Применим это всё при вычислении получившегося интеграла.
Пределы интегрирования изменятся так:
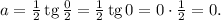
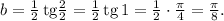
Вычислим теперь сам интеграл:
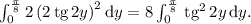
Введём замену: 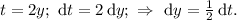
Пределы интегрирования изменятся так:
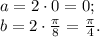
Продолжим вычисление интеграла:
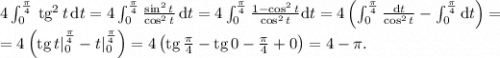
Подставим найденное значение в выражение после интегрирования по частям и найдём итоговый результат:
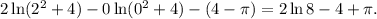
Наконец, получаем, что 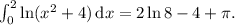
а) 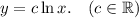
б) 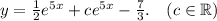
Пошаговое объяснение:
а) Начнём с классификации ДУ. Это ДУ первого порядка, первой степени, линейное, обыкновенное.
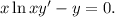
В таком случае подойдёт замена 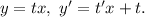 Введём её:
Введём её:
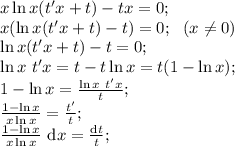
Удалось разделить переменные. Проинтегрируем обе части уравнения:
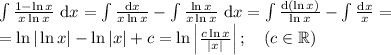
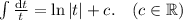
Приравняем и упростим обе части уравнения:
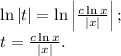
Обратная замена:
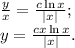
Логарифм от  существует только тогда, когда
существует только тогда, когда 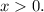 Модуль
Модуль 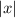 для
для 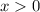 равен самому
равен самому  , поэтому:
, поэтому:
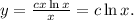
б) Начнём с классификации ДУ. Это ДУ первого порядка, первой степени, линейное, обыкновенное.
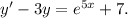
Введём переменную 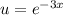 и домножим на неё обе части уравнения:
и домножим на неё обе части уравнения:
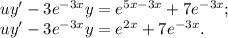
Отметим, что 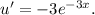 Зная это, упростим:
Зная это, упростим:
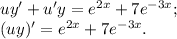
Удалось разделить переменные. Проинтегрируем обе части уравнения:
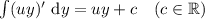
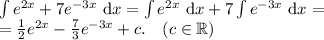
Обратим замену, приравняем выражения и упростим:
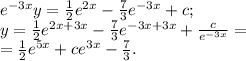
Пошаговое объяснение:
Скорость катера плывущего по реке равна 20,4+2,5=22,9 км/ч. Значит по течению реки он км.
Скорость катера плывущего против течения реки 20,4-2,5=17,9 км/ч. Значит против течения он км.
Весь путь катера составил 34,35+32,22=66,57 км
1) 2,7/0,6= 4,5 (км/ч) скорость пешком.
2)4,5+6,3=10,8(км/ч) скорость на велосипеде.
3) 2,7/10,8=0,25(ч)
ответ: За 0,25 часа Андрей проезжает растояние 2,7 км на велосипеде. :)