область определения функции это допустимые значения х. те вопрос можно сформулировать - при каких значениях х выполнимы все действия. записанные в формуле функции. разберем на примерах:
у=кх+в линейная функция. действия: умножение К*х и сложение ( вычитания. все действия выполнимы. в общем случае Д (Х) от минус до плюс бесконечности.
у=к\х деление на ноль не допускается. тч Д (х) х не равен нулю
для у=Vx, где буква V как знак квадратного корня Д (х) х больше или равен нулю.
Для у=ах"2+вх+с и у =ах"3 область определения от минус до плюс бесконечности. тк все действия выполнимы.
z = (x-2)^2+2*y^2-10
1. Найдем частные производные.
На фото
2. Решим систему уравнений.
2*x-4 = 0
4*y = 0
Получим:
а) Из первого уравнения выражаем x и подставляем во второе уравнение:
x = 2
4*y = 0
Откуда y = 0
Данные значения y подставляем в выражение для x. Получаем: x = 2
Количество критических точек равно 1.
M1(2;0)
3. Найдем частные производные второго порядка.
На фото
4. Вычислим значение этих частных производных второго порядка в критических точках M(x0;y0).
Вычисляем значения для точки M1(2;0)
На фото
AC - B2 = 8 > 0 и A > 0 , то в точке M1(2;0) имеется минимум z(2;0) = -10
Вывод: В точке M1(2;0) имеется минимум z(2;0) = -10;
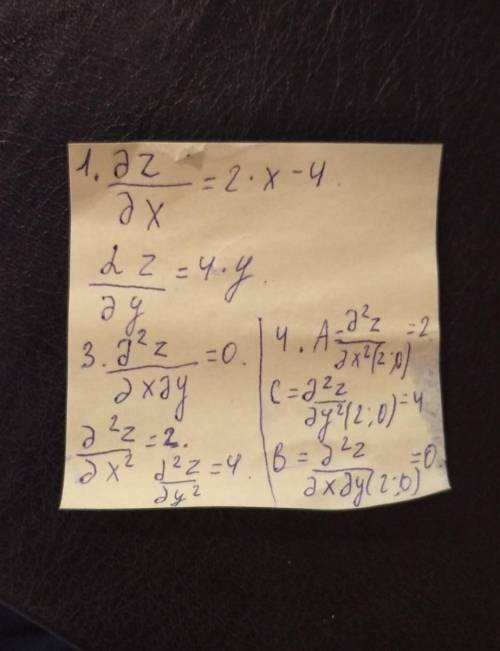
ответ: пусть длина меньшей стороны равна х. тогда х*(х+2)=х²+2*х=168⇒х²+2*х-168=0⇒ дискриминант D=4+4*168=676 корни х1=(-2+26)/2=24/2=12 метров х2=(-2-26)/2 - значение не подходит по смыслу задачи.
1. Вычисли длину и ширину детской площадки.
Меньшая сторона детской площадки (целое число) равна: х=12 м.
Большая сторона детской площадки (целое число) равна: х+2=14 м.
2. Вычисли, сколько упаковок материала для бордюра необходимо купить.
Необходимое количество упаковок равно: необходимая длина бордюра равна 2*(12+14)=52 метра или 52/10=5,2 округляем до целого большего 6 упаковок.
Пошаговое объяснение: