Треугольник АВС - прямоугольный с прямым углом С. Более того он египетский - это серия треугольников в которых необязательно применять теорему Пифагора для вычисления одного из неизвестных катетов или гипотенузы. Это треугольник 3, 4, 5, то есть сторона ВС равна 3.
а) Синус 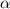 - это отношение катета, лежащего напротив угла
- это отношение катета, лежащего напротив угла 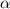 к гипотенузе. В данном случае
к гипотенузе. В данном случае 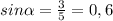 .
.
б) Косинус 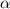 - это отношение катета, прилежащего к углу
- это отношение катета, прилежащего к углу 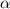 к гипотенузе. В данном случае
к гипотенузе. В данном случае 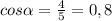 .
.
в) Тангенс 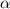 - это отношение противолежащего катета к прилежащему катету. В данном случае
- это отношение противолежащего катета к прилежащему катету. В данном случае  .
.
г) Котангенс 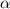 - это отношение прилежащего катета к противолежащему катету. В данном случае
- это отношение прилежащего катета к противолежащему катету. В данном случае 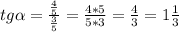 .
.
В этот раз я не могу точно сказать длину катета ВС, так как он не египетский. Найдём длину катета ВС:
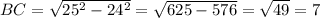 см.
см.
а) Синус А - это отношение катета, лежащего напротив угла А к гипотенузе. В данном случае 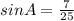 .
.
б) Косинус A - это отношение катета, прилежащего к углу A к гипотенузе. В данном случае 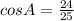 .
.
в) Тангенс B - это отношение противолежащего катета к прилежащему катету. В данном случае 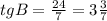 .
.
г) Котангенс В - это отношение прилежащего катета к противолежащему катету. В даннм случае 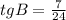 .
.
д) tg B · ctg B = 1. Произведение тангенса и котангенса всегда равно 1.
е) sin²A + cos²A = 1. Сумма квадратов синуса и косинуса угла всегда равна 1. (Также как и в предыдущем случае, это одна из аксиом (свойств, не требующих доказательств).