В полдень обе стрелки часов показывают на 12. Затем минутная стрелка сделает полный оборот, а часовая будет показывать 1 час. Пока минутная стрелка повернётся к 1(пройдёт 5 минут), часовая опять чуть-чуть убежит вперёд. Так что обе стрелки встретятся ещё раз через 1 час, 5 минут и ещё какое-то количество секунд.
А теперь строгие вычисления.
Угловая скорость часовой стрелки (полный оборот 360° за 12·60·60c)
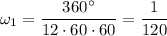 °/c
°/c
Угловая скорость минутной стрелки (полный оборот 360° за 60·60c)
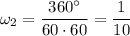 °/c
°/c
Пусть стрелки в следующий раз встретятся через время t, за которое минутная стрелка успеет сделать на целый оборот больше, чем часовая.
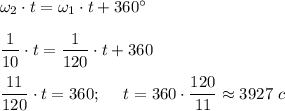
t = 3927 с = 65 мин 27 с
ответ: стрелки встретятся примерно через 1 час 5 минут 27 секунд
Правильную последовательность длины 2n можно получить так:
1) Выбрать произвольное k с условием 0≤k≤n-1.
2) Между 1 и -1 вставить любую правильную последовательность длиной 2k.
3) К полученной последовательности приписать правильную последовательность длиной 2(n-k-1). При этом, если надо приписывать или вставлять последовательность нулевой длины, то ничего не делаем.
В итоге, получается последовательность длиной 2+2k+2(n-k-1)=2n. Причем, эта последовательность обязательно правильная, т.к.
a)
б)
в)
Обратное тоже верно. Любую правильную последовательность длины 2n можно представить в таком виде. Действительно, в качестве k можно выбрать первое такое k, что
Из этого построения следует рекуррентная формула для числа всех правильных последовательностей длины 2n. Обозначим через
Здесь первое слагаемое соответствует k=0, т.е.это количество всех правильных последовательностей вида {1,-1, произвольная правильная последовательность длины 2(n-1)}.
Второе слагаемое соответствует k=1, когда последовательности имеют вид
{1, все правильные последовательности длины 2, -1, все правильные последовательности длины 2(n-2)}. И т.д.
Итак, для n=7:
ответ: 429.
P.S. Полученное рекуррентное соотношение можно упростить, и доказать, что