1. НОК (25, 255) = 1275
2. НОК (96, 256) = 768
3. НОК (32, 48) = 96
Пошаговое объяснение:
Наименьшее общее кратное (НОК) - это наименьшее натуральное число, которое само делится нацело на каждое из этих чисел:
1. 25 и 255
Разложим на простые множители сначала число 25 : 25 = 5* 5
Затем число 255 : 255 = 5 * 3 * 17
Далее, выберем в разложении меньшего числа (25) множители, которые не вошли в разложение большего числа: это 5 .
Добавим этот множитель в разложение большего числа (255)
5, 3, 17 , 5 и перемножив эти числа, полученное произведение запишем в ответ:
НОК (25, 255) = 5 * 3 * 17 * 5 = 1275
Далее точно по такому же принципу.
2. 96 и 256
96 = 2 * 2 * 2 * 2 * 2 * 3
256 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2
НОК (96, 256) = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 3 = 768
3. 32 и 48
32 = 2 * 2 * 2 * 2 * 2
48 = 2 * 2 * 2 * 2 * 3
НОК (32, 48) = 2 * 2 * 2 * 2 * 2 * 3 = 96
Рисунок во вложении.
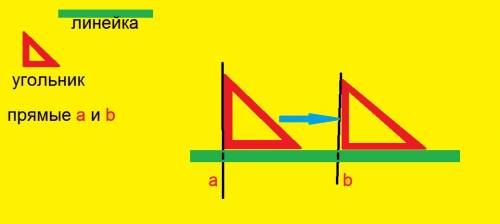
1. Нарисовать две прямые а и b.
2. Совместить сторону (катет) прямого угла угольника с прямой а, а к другой стороне (катету) приложить линейку.
3. Двигать угольник по линейке до прямой b.
4. Проверить, если та сторона, которая была совмещена с прямой а, совмещается, также, и с прямой b.
Если совмещается, то прямые параллельны, если нет - то не параллельны.
На рисунке видно, что сторона угольника не совместилась с прямой b, значит эти прямые не параллельны.
ответ: построение параллельных прямых неточное, a ∦ b.
При данной проверке подтвеждается правило параллельности прямых: " Если две прямые на плоскости перпендикулярны третьей прямой, то они параллельны."
В роли третьей прямой выступает линейка, а угольник проверяет, если углы пересечения прямых а и b с линейкой равны.
1) 5.
2) 2
3) 2
Пошаговое объяснение:
В первом случае кратное чисел 25 и 255 будет 5
Во втором случае кратное чисел 96 и 256 будет 2
И в третьем случае кратное чисел 32 и 48 будет 2