Дроби приводятся к одному знаменателю, числители складываются
Например:
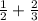приводим к общему знаменателю 6, умножая первую дробь на 3, вторую на 2, получаем: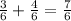 
Десятичные числа:
те же дроби в виде десятичного числа:
0,5+0,66=1,16
2) Вычитание проводим аналогичным , как и сложение
3) Умножениечислитель умножается на числитель, знаменатель на знаменатель
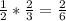
переворачиваем дробь и умножаем
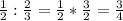
Дроби: числитель в степень, знаменатель в степень
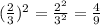
Десятичные числа: не обращаем внимания на ноль, возводим в степень после запятой
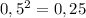
(-+) означает, что ставится знак того числа, которое по модулю больше
Например: (-)8+(+)13=(+)5
(+)20-40=(-)20
Не имеет значения, какое число первое, отрицательное или положительное, результат тот же, что в правиле
(-)*(+)=(-) и так же (+)*(-)=(-)
Все действия аналогично
\frac{3}{7}73 ÷ k = 5 ÷ 2\frac{1}{3}231
\frac{3}{7}73 ÷ k = 5 × \frac{3}{7}73
k = \frac{3}{7}73 ÷ \frac{15}{7}715
k = \frac{3*7}{7*15}7∗153∗7
k = \frac{1}{5}51
k = 0,2
2) 5,5 ÷ 8 = k ÷ \frac{2}{11}112
\frac{11}{2}211 × \frac{1}{8}81 = k ÷ \frac{2}{11}112
k = \frac{11*2}{16*11}16∗1111∗2
k = \frac{1}{8}81
k = 0,125
3) k ÷ \frac{5}{9}95 = 1\frac{4}{5}154 ÷ 6
k ÷ \frac{5}{9}95 = \frac{9}{5*6}5∗69
k = \frac{5*3}{9*10}9∗105∗3
k = \frac{1}{6}61
4) 20 ÷ 3\frac{1}{4}341 = \frac{4}{13}134 ÷ k
\frac{20*4}{13}1320∗4 = \frac{4}{13}134 ÷ k
k = \frac{4*13}{13*80}13∗804∗13
k = \frac{1}{20}201
k = 0,05
сори,без понятия как решить без икса