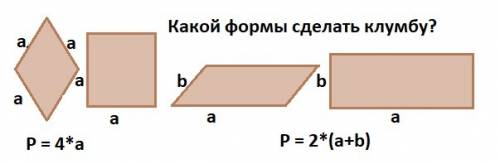
В задаче не сказано какой формы будут клумбы - вот и задумался садовник. Рисунок к задаче в приложении.
Если стороны равны - а , то это ромб или квадрат. Тогда периметр по формуле: Р = 4*а.
Если стороны разные: a и b, то это параллелограмм или прямоугольник и периметр по формуле: P = 2*(a + b).
1) а = b = 4 м. Р1 = 4*а = 4*4 = 16 м - периметр первой клумбы.
2) Р2 = 2*(6 + 4) = 2*10 = 20 м - периметр второй клумбы
3) Р3 = 2*(7 + 2) = 2*9 = 18 м - периметр третьей клумбы.
4) Р4 = 2*(5 + 3) = 2*8 = 16 м - периметр четвёртой клумбы.
И теперь длину изгороди на все четыре клумбы - сумма отдельных.
5) Р = 16+20+18+16 = 70 м на все четыре клумбы - ОТВЕТ
1) 2,4:8
нужно умножить оба числа на 10
24:80
первое фото
2)0,42:7
нужно умножить оба числа на 100
42:700
второе фото
3)5,5:5
нужно умножить оба числа на 10
55:50
третье фото
4)0,048:12
нужно умножить оба числа на 1000
48:12000
четвертое фото
5)7:2
пятое фото
6)5,36:6
нужно умножить оба числа на 100
536:600
дальше нельзя добавлять вложения!если получится напишу ответы дальше в комментарии к этому ответуесли не сложно,поставь лучший
_________
в комментарии нельзя добавлять вложения(((
сейчас ещё попробую ((
не получается
но я старалась,поставь лучший
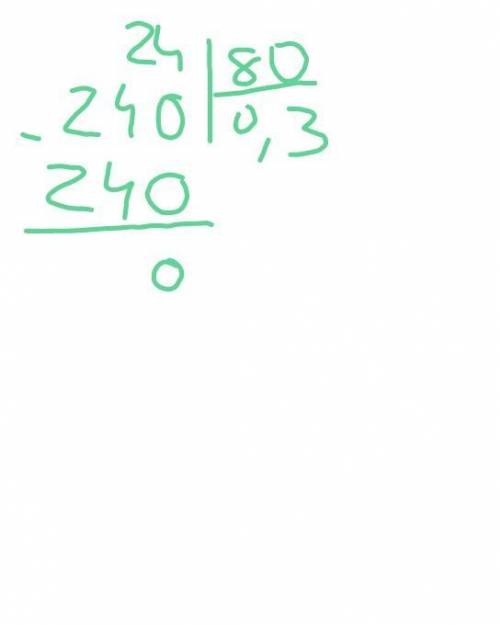
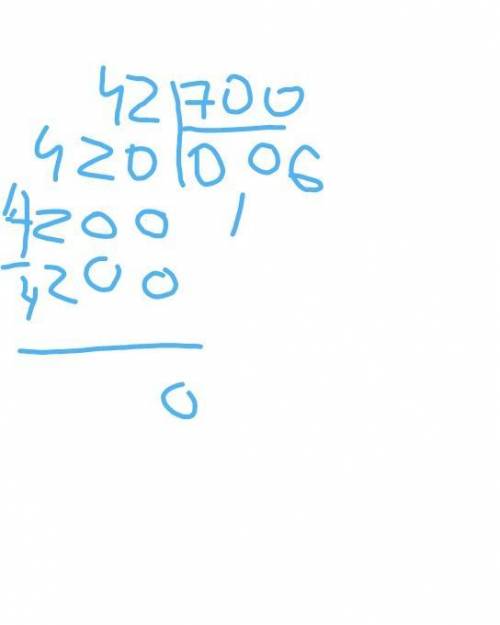
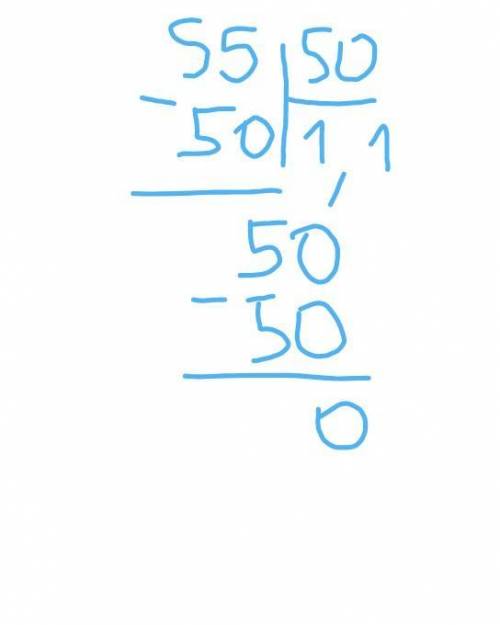
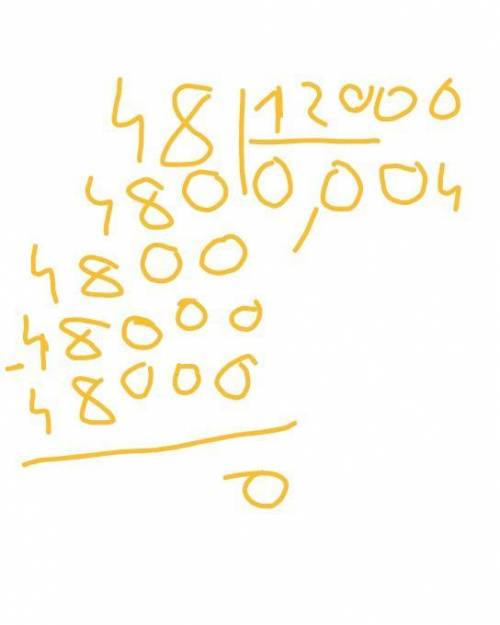
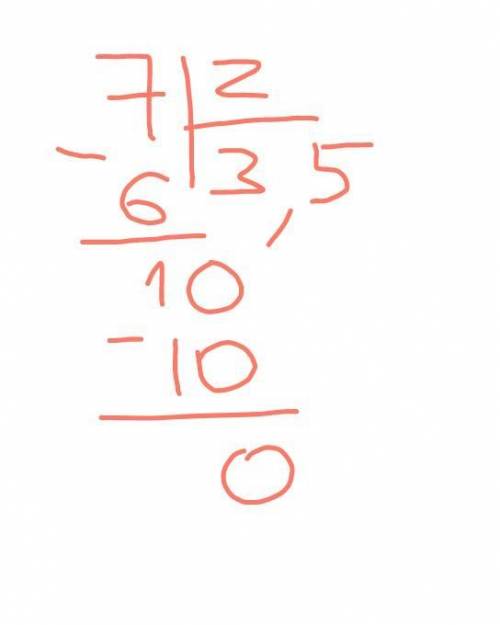
Дано: y = x² - 3*x + 2
ИССЛЕДОВАНИЕ.
1. Область определения (ООФ) D(y) = R, Х∈(-∞;+∞) - непрерывная , гладкая
2. Пересечение с осью OХ. Решаем квадратное уравнение.
y(x) = (x-1)*(x-2) = 0
Нули функции: х1 = 1 и х2 = 2.
3. Интервалы знакопостоянства. Положительная парабола, ветви вверх.
Положительна - y(x)>0 - x∈(-∞;1)∪(2;+∞).
Отрицательна - y(x)≤0 -x∈[1;2]
4. Пересечение с осью OY. Y(0) = 2
5. Исследование на чётность.
Y(-x) ≠ Y(x) - не чётная. Y(-x) ≠ -Y(x), Функция ни чётная, ни нечётная.
6. Первая производная. Y'(x) = 2*x - 3 = 0
x = 1.5 - точка экстремума.
7. Локальный экстремум.
Ymin(1.5) = - 0.25
8. Интервалы возрастания и убывания.
Убывает - Х∈(-∞;1,5]. Возрастает - Х∈[1.5;+∞)
9. Вторая производная - Y"(x) = 2.
10. Точек перегиба нет. Вогнутая ("ложка") во всей ООФ.
11. Область значений - Е(у) - У∈[-0.25;+∞)
12. График в приложении.