В решении.
Пошаговое объяснение:
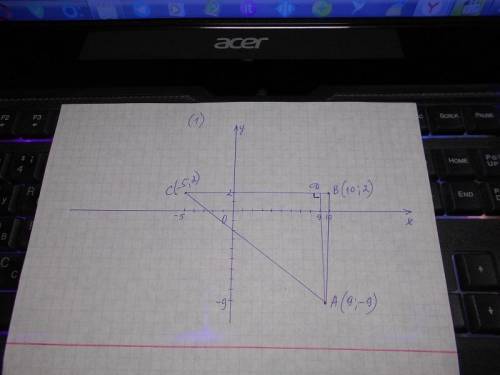
1. Найдите площадь треугольника АВС с вершинами А(9;-9), В(10;2), С(-5;2).
Построить треугольник по заданным точкам. Из точки А опустить перпендикуляр АD на основание СВ.
S треугольника = 1/2 основания * h;
Основание = СВ = 5 + 10 = 15 (ед.);
h = АD = 9 + 2 = 11 (ед.);
S треугольника АВС = 1/2 * 15 * 11 = 82,5 (ед.²).
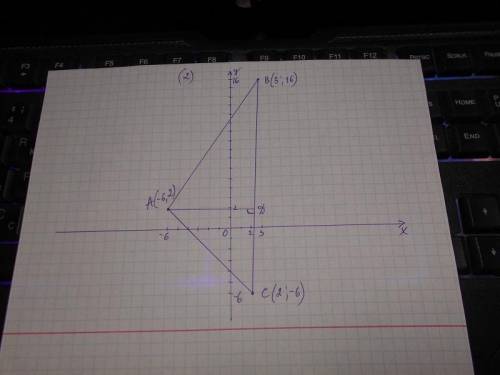
2) Найдите площадь треугольника АВС с вершинами А(-6;2), В(3;16), С(2;-6).
Построить треугольник по заданным точкам. Из точки А опустить перпендикуляр АD на основание СВ.
S треугольника = 1/2 основания * h;
Основание = СВ = 22,2 (ед.);
h = АD = 8,4 (ед.);
S треугольника АВС = 1/2 * 22,2 * 8,4 = 93,24 (ед.²).
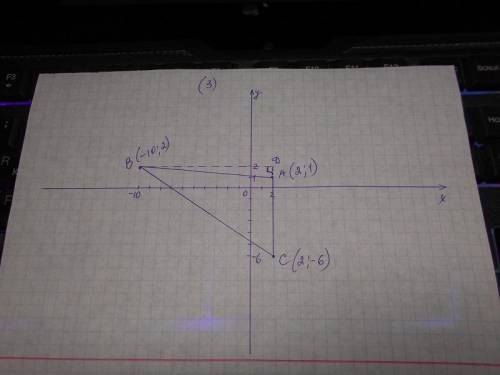
3) Найдите площадь треугольника АВС с вершинами А(2;1), В(-10;2), С(2;-6).
Построить треугольник по заданным точкам. Из точки В опустить перпендикуляр АD на продолжение основания АС.
S треугольника = 1/2 основания * h;
Основание = АС = 1 + 6 = 7 (ед.);
h = ВD = 10 + 2 = 12 (ед.);
S треугольника АВС = 1/2 * 7 * 12 = 42 (ед.²).
n = 10
Пошаговое объяснение:
(n! + (n+2)!) / (n+1)! = 133/11
Заметим, что:
(n+1)! = n!*(n+1)
(n+2)! = n!*(n+1)(n+2)
Подставляем в уравнение.
(n! + n!*(n+1)(n+2)) / (n!*(n+1)) = 133/11
Сокращаем n!
(1 + (n+1)(n+2)) / (n+1) = 133/11
(1 + n^2 + 3n + 2) / (n+1) = 133/11
По правилу пропорции
11(n^2 + 3n + 3) = 133(n+1)
11n^2 + 33n + 33 = 133n + 133
11n^2 - 100n - 100 = 0
D = 100^2 - 4*11(-100) = 10000 + 4400 = 14400 = 120^2
n1 = (100 - 120)/22 = -20/22 < 0 - не подходит
n2 = (100 + 120)/22 = 220/22 = 10 - подходит.
.....................................