Пошаговое объяснение:
у=х⁴-2х²+1
1) Область определения функции.
D(f) = R
2) Находим производную функции.
у' = 4х³-4х
3)Найдем нули производной:
y' = 0;
4х³-4х=0
4х(х²-1)=0,
х₁=0, х₂=1, х₃=-1
4) Получилось четыре промежутка:
(-∞; -1), (-1; 0), (0; 1) и (1; +∞).
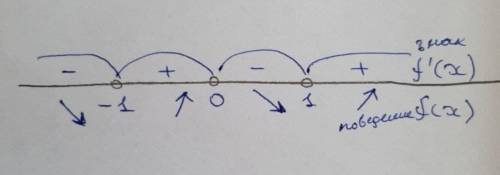
5) Расставим знаки производной на каждом промежутке:
(-∞; -1) если х = -10: y'(-10) = 4 * (-10)³ - 4 * (-10) <0 (минус).
(-1; 0) если х = -1/2: y'(-1/2) = 4 * (-1/2)³ - 4 * (-1/2) = -4/8 + 2 = 1,5 >0 (плюс).
(0; 1) если х = 1/2: y'(1/2) = 4 * (1/2)³ - 4 * (1/2) = 4/8 - 2 = -1,5 <0 (минус).
(1; +∞) если х = 3: y'(2) = 4 * 3³ - 4 * 3 = 108 - 12 = 96 >0 (плюс).
6)Определяем промежутки возрастания и убывания функции:
Если знак производной функции на промежутке положительный, то функция возрастает, если отрицательный - то убывает.
Функция возрастает (производная плюс) на (-1; 0) и (1; +∞).
Функция убывает на (-∞; -1) и (0; 1).
В решении.
Пошаговое объяснение:
Лодка по течению реки 5 км и против течения 6 км, затратив на весь путь 7 часов. Скорость течения 2 км/ч, какова собственная скорость лодки?
Формула движения: S=v*t
S - расстояние v - скорость t – время
х - собственная скорость лодки.
х + 2 - скорость лодки по течению.
х - 2 - скорость лодки против течения.
5/(х + 2) - время лодки по течению.
6/(х - 2) - время лодки против течения.
По условию задачи уравнение:
5/(х + 2) + 6/(х - 2) = 7
Умножить все части уравнения на (х + 2)(х - 2), чтобы избавиться от дробного выражения:
5*(х - 2) + 6*(х + 2) = 7*(х + 2)(х - 2)
Раскрыть скобки:
5х - 10 + 6х + 12 = 7х² - 28
Привести подобные:
-7х² + 11х + 30 = 0/-1
7х² - 11х - 30 = 0, квадратное уравнение, найти корни:
D=b²-4ac =121 + 840 = 961 √D=31
х₁=(-b-√D)/2a
х₁=(11-31)/14 = -20/14, отбросить, как отрицательный.
х₂=(-b+√D)/2a
х₂=(11+31)/14
х₂=42/14
х₂=3 (км/час) - собственная скорость лодки.
Проверка:
5/5 + 6/1 = 1 + 6 = 7 (часов), верно.