10 раз команда могла проиграть
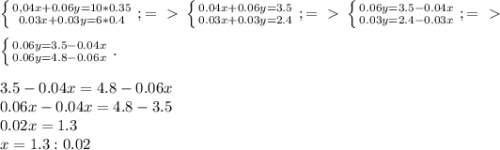
2 раза
Пошаговое объяснение:
Разделы теорииКликните, чтобы открыть меню Главная > Классическое определение вероятности Классическое определение вероятности 1. Читай полную теорию 2. Вникай в доказательства 3. Применяй на практике Факт 1. Случайное событие – это событие, которое при данных условиях может произойти, а может не произойти. Например, событие “при бросании игральной кости выпало 3 или 4 очка”. Напомним, что игральная кость – это кубик с шестью гранями, на которых написаны числа от 1 до 6. Предположим, что мы проводим некоторое испытание (эксперимент), например, бросаем игральную кость. Результатом нашего испытания может быть одно из шести событий: выпадет 1 очко, выпадет 2 очка, 3 очка, 4 очка, 5 очков или 6 очков. Такие события называются элементарными событиями (то есть это “простейшие” события, которые в совокупности образуют все множество исходов нашего эксперимента). Например, событие “при бросании игральной кости выпало 3 или 4 очка” не является элементарным, оно состоит из двух элементарных событий “при бросании игральной кости выпало 3 очка” и “при бросании игральной кости выпало 4 очка”. Если сложить вероятности всех возможных элементарных событий у некоторого эксперимента, то получится 1. Два события мы будем называть равновероятными (равновозможными), если вероятности наступления любого из них одинаковы. Например, при бросании игральной кости вероятности любого из событий: выпадет 1 очко, выпадет 2 очка, 3 очка, 4 очка, 5 очков или 6 очков, одинаковы. Или, например, при подбрасывании монеты вероятности событий “выпадет орел” и “выпадет решка” также одинаковы. Примером неравновероятных событий могут послужить два события: “при бросании игральной кости выпадет 1 очко” и “при бросании игральной кости выпадет нечетное количество очков”. Почему? В первом случае нам удовлетворяет только исход, когда кубик упадет кверху гранью, на которой написано 1; во втором случае нам подходит целых три исхода: он может выпасть кверху гранью.
В футболе команда получает за победу 3 очка,за ничью -1очко,за поражение -0 очков.Команда сыграла 38 матчей и получила 80 очков.Какое наибольшее число раз эта команда могла проиграть? 8,9,10,11,12,???
Решение Определим минимальное количесво игр результат которых не равен нулю и это число должно делится на 3 без остатка (по правилу: если сумма цифр числа делится на 3 без остатка, значит и число делится без остатка):
ближайшие числа (к 80) которое делится на 3 без остатка являются: 78 и 81. Число 81 не рассматриваем, т.к. очков всего 80, тогда число выйгрышных очков равно 78 и проведено выигрышных игр: 78/3=26, тогда число очков которые получены в результате ничьей равны 80-78=2, тогда всего игр за которые получены очки равно: 26+2=28. Тогда значит максимальное число проигрышных партий равно: 38-28=10.
ответ: максимальное число проигранных партий равно провели выигрышных игр
20
18
2 (остаток)
2/1=2 - провели игр с результатом "ничья"
38-(26+2)=10 - максимальное число игр в которых команда проиграла