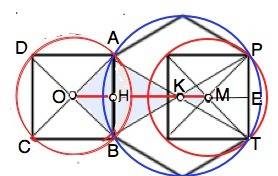
Центры окружностей могут быть расположены как по разные стороны от данной хорды, так и по одну. (см. рисунок)
Вариант 1.
Квадрат АВСD вписан в окружность с центром О, правильный шестиугольник вписан в окружность с центром К.
Сторона АВ общая и является хордой обеих окружностей.
Радиус окружности. описанной около квадрата, равен половине его диагонали. Диагонали квадрата пересекаются под прямым уuлом и делят его на равнобедренные прямоугольные треугольники.
Тогда сторона АВ ( она же хорда) равна АО:sin 45°=10√2.
Правильный шестиугольник состоит из 6 правильных треугольников, сторона которых равна радиусу описанной около шестиугольника окружности.
Искомое расстояние ОК=ОН+КН
ОН=АВ:2=5√2
KH=AK•sin 60°=5√6
ОК=5√2+5√6=5√2•(1+√3)= ≈9,8 см
Вариант 2.
Центры окружностей расположены по одну сторону от общей хорды РТ.
Радиус описанной окружности квадрата и длина хорды ( и сторона квадрата) те же, что в варианте 1.
Центр большей окружности К, меньшей - М.
Искомое расстояние - длина отрезка КМ.
КМ=КЕ-МЕ
КМ=5√6-5√2=5√2•(√3-1)= ≈5,176 см.
[1]
,Фараб
[2]
[3]
— между 14 декабря 950
и 12 января 951
,Дамаск
[2]
) — философ, математик, теоретик музыки, ученый Востока. Один из крупнейших
восточной философии
. Аль-Фараби — автор комментариев к сочинениям Аристотеля
(отсюда его почётное прозвище «Второй учитель») иПлатона
. Его труды оказали влияние наибн Сину
, ибн Баджу
, ибн Туфайля
, ибн Рушда
, а также на философию и науку средневековой Западной Европы. Ему приписывается создание Отрарской библиотеки