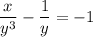В решении.
Пошаговое объяснение:
Определите вид зависимости величин и решите задачу с
составления пропорции.
С одинаковых труб бассейн заполняется водой за 25 минут. За сколько минут можно заполнить бассейн с таких труб?
Пропорция:
8 (труб) - 25 (минуты)
10 (труб) - х (минут)
Зависимость обратно пропорциональная ( чем больше труб, тем меньше времени понадобится):
8/10 = х/25
По основному свойству пропорции (произведение её крайних членов равно произведению средних членов):
х=8*25:10
х=20 (минут).
Данное дифференциальное уравнение перепишем в следующем виде
где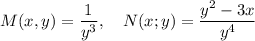
Тогда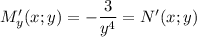 , что собственно можем сделать вывод, что данное диф. уравнение является уравнением в полных дифференциалах
, что собственно можем сделать вывод, что данное диф. уравнение является уравнением в полных дифференциалах
Если функция F(x;y) удовлетворяет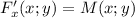 и
и 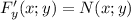 , то
, то 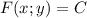 - решение дифференциального уравнения
- решение дифференциального уравнения
Интегрируем по переменной х
далее продифференцируем по переменной у
Откуда общий интеграл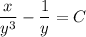
Найдем частный интеграл, подставляя начальные условия
Частный интеграл: