12; 48
Пошаговое объяснение:
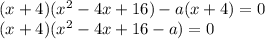
Уравнение обязательно имеет одно решение: x = -4. Квадратное уравнение во второй скобке может иметь 0, 1 или 2 решения. Очевидно, нужно рассматривать последние два случая.
1. Если квадратное уравнение имеет одно решение, то оно должно отличаться от x = -4, так как требуется найти два различных решения.
2. Если квадратное уравнение имеет два решения, то одно из них должно равняться x = -4.
Случай 1: 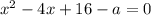 — 1 решение.
— 1 решение.
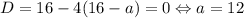
При a = 12 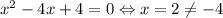 — подходит.
— подходит.
Случай 2: 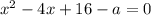 — 2 решения, одно из них x = -4.
— 2 решения, одно из них x = -4.
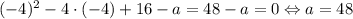
При a = 48 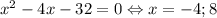 — подходит.
— подходит.
a∈(-∞;-5)U(-5;0)U(0;3)U(3;4)U(4;5)
Объяснение:

Воспользуемся формулой 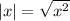 :
:
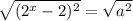
Возведем обе части в квадрат:
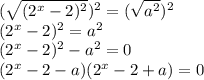
Рассмотрим 3 случая :
1.
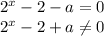
----------------------
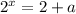
Мы знаем, что любое число(кроме 0) в любой степени больше нуля, то есть 2+а > 0 => a>-2
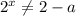
Так же 2-а уже должно быть меньше или равно нулю:
2-a ≤ 0 => a ≥ 2
Найдем пересечение => a ≥ 2
2.
По тому же принципу :
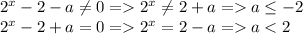
Найдем пересечение => a ≤-2
3.
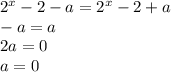
----------------------------------------------------------------------
Объединим три ответа => a Є (-∞ ; -2] U [2 ; +∞)
ответ : a Є (-∞ ; -2] U [2 ; +∞) U {0}
P.S это одно из возможных решений, возможно вы найдете и по проще)
Запомнив, что 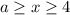 перепишем уравнение как
перепишем уравнение как
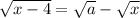
и возведем в квадрат:
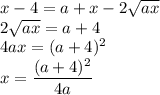
Последний переход справедлив, так как a!=0.
Проверим условие a>=x:
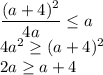
Неравенство, как и следовало ожидать, выполняется при всех a>=4.
Итак, уравнение имеет ровно 1 корень при a>=4, равный (a+4)^2/4a.
ответ. Такого а не существует.
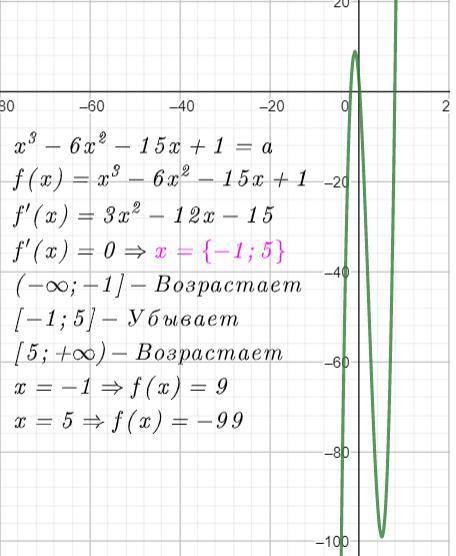
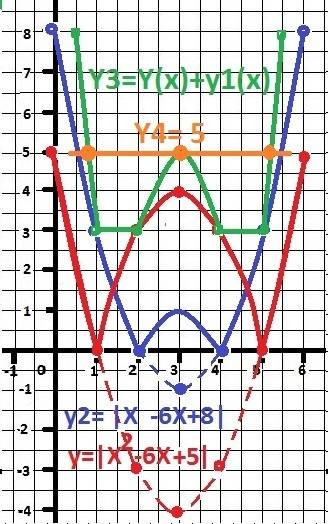
После того,как мы нашли промежутки возрастания и убывания. Нужно найти значения функции в данных точках (-1 и 5). После этого мы можем уже построить график и убедиться,что три решения будет на промежутке [-99;9]
Это биквадратное уравнение, стандартно имеет 4 решения, а 2 только в вырожденном случае, когда трёхчлен - полный квадрат, то есть d^2=49, d=+-7.
В этом случае получается
(x^2-7)^2=0, то есть эти 2 различных корня
x=+-sqrt(7)
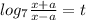 и получим уравнение
и получим уравнение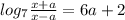
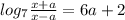
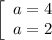
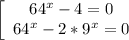
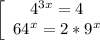
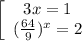
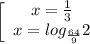
От репродуктивного здоровья в подростковом возрасте во многом зависит дальнейшая полноценная жизнь наших детей. Так, вовремя замеченная и вылеченная проблема лишит его проблем с деторождением во взрослом возрасте.
И охрана репродуктивного здоровья подростков должны начинаться еще с охраны здоровья школьников и даже более младших детей. Прежде всего, забота о репродуктивном здоровье детей и подростков лежит на их родителях.
Не нужно ждать определенного возраста, например, 14 лет, чтобы показать свою дочь гинекологу или положиться на школьный медосмотр. Начинать заботу о здоровье половой системы детей нужно с самого рождения.
Репродуктивное здоровье девочки – это, прежде всего, грамотная гигиена половых органов. Впрочем, это касается и мальчиков. При возникновении подозрений на воспалительные процессы нужно немедленно обращаться к специалистам – хирургу и детскому гинекологу.
При наступлении же у девочек первых месячных, она должна быть подготовлена к этому. Потому что замечено, что примерно каждая третья девочка с самого начала полового созревания сталкивается с нерегулярными менструациями и прочими сопутствующими проблемами. Но из-за стеснения не обсуждает это с мамой и тянет эту проблему в подростковый, а потом и во взрослый период своей жизни. И это становится причиной различной сложности проблем, вплоть до бесплодия у женщин, когда они ими станут.
Не менее важно обращать внимание своих детей на влияние курения и спиртного на репродуктивное здоровье. Нужно в доступной форме и без нажима объяснить своему сыну или дочери, как опасен табак и алкоголь, как пагубно эти вредные привычки влияют на половое здоровье и на рождение здоровых детей.
х^2-10х+а^2=(х-5)(х+5)
а=5 и а=-5
х^2-10х+25
d=√(-10)^2-4*25=0
x1=10/2=5
x2=-5
ответ: 5 и (-5)