Уюли были маркеры, у вари на 10 маркеров больше чем у юли, а у светы на два маркера меньше чем у юли. всего было 40 маркеров сколько маркеров была у юли, вари и светы? решите уравнением и словами пусть, было, всего. ​

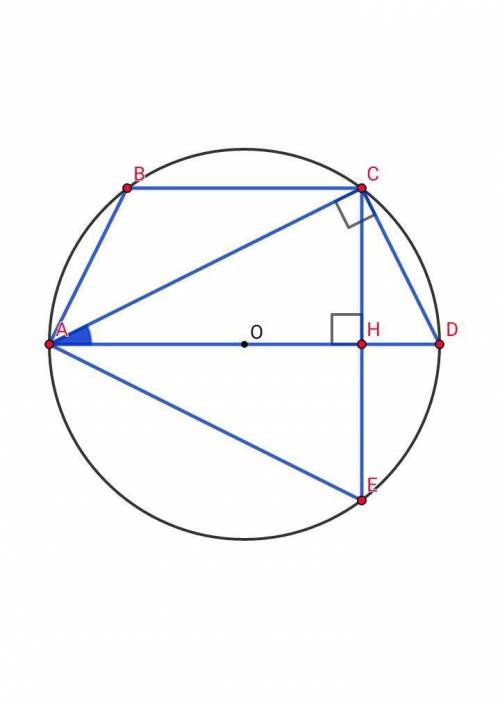
У Юли 10 2/3

У Вари 20 2/3

У Светы 8 2/3

Пошаговое объяснение:

Всего было 40 маркеров.У Юли,у Вари больше на 10,чем у Юли,у Светы на два маркера меньше,чем у Юли.

Пусть маркеры Юли будет х,только у Вари было х+10 маркеров,а у Светы было х-2 маркеров.

Составим уравнение

х + х + 10 + х - 2 = 40

х оставляем в левой части,числа переносим в правую

х + х + х = 40 - 10 + 2

3х = 32

х = 32 : 3

x = 10 2/3

Значит у Юли было 10 2/3 маркеров,у Вари 10 2/3 + 10 = 20 2/3 маркеров,а у Светы 10 2/3 - 2 = 8 2/3 маркеров

10 2/3 + 20 2/3 + 8 2/3 = 40

всё сделано правильно.

ответ:

12-(5+3) =4

пошаговое объяснение:

ответ:

пошаговое объяснение:

981: 9•6-16•30: 5+172•2=902

981: 9=109

109*6=654

16•30=480

480: 5=96

172•2=344

654-96=558

558+344=902

800-50•9: 3•6: 300•69=593

50•9=450

450: 3=150

150*6=900

900: 300=3

3*69=207

800-207=593