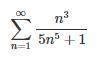
Пошаговое объяснение:
используем признак сравнения
рассмотрим предел общего члена
упростим его
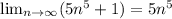
тогда исходный ряд можно представить в виде
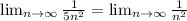
а это обобщенный гармонический ряд с α > 1
тогда и исходный ряд сходится.
1.
а) 1/4
б) - 11/30 (вся дробь отрицательная)
в) - 1/3 (вся дробь отрицательная)
Г) - 2/3 ( вся дробь отрицательная)
2.
- 7/60 (вся дробь отрицательная)
3.
а) - 7/11 (вся дробь отрицательная)
б) 1/2
4.
Вся работа =1.
Первая бригада в час делает 1/16 всей работы.
Вторая бригада делает в час 1/48 всей работы.
Вместе за 1 час обе бригады выполнят 1/16 + 1/48 = 3/48 + 1/48 = 4/48 = 1/12 всей работы.
Теперь ищем время. 1: 1/12 = 12(час.)
5.
1)1/9 часть бака наполнена за 1 мин двумя кранами
2)1/36 часть бака наполнена за 1 мин первым краном
3) 1/9 - 1/36 = 4-1/36 = 3/36 = 1/12 часть бака наполнена за мин вторым краном
4) 1:1/12 = за 12 мин наполнится бак вторым краном
Надеюсь правильно, если что пишите
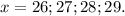
Пошаговое объяснение:
Обыкновенная дробь называется правильной, если ее числитель меньше знаменателя.
Обыкновенная дробь называется неправильной, если ее числитель больше или равен знаменателю.
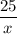 - правильная дробь. Тогда
- правильная дробь. Тогда 
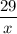 - неправильная дробь. Тогда
- неправильная дробь. Тогда 
Оба условия будут выполняться, если 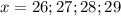
При х=26 дробь 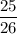 - правильная, а дробь
- правильная, а дробь 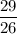 неправильная.
неправильная.
При х=27 дробь 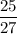 - правильная, а дробь
- правильная, а дробь 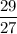 неправильная.
неправильная.
При х=28 дробь 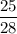 - правильная, а дробь
- правильная, а дробь 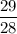 неправильная.
неправильная.
При х=29 дробь 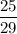 - правильная, а дробь
- правильная, а дробь 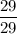 неправильная.
неправильная.
Відповідь:
ряд збігається
Покрокове пояснення:
Знайдемо границю n+1 члена ряду до n-го при n→бескінечності
(n+1)^3/(5(n+1)^5+1) : n^3/(5n^5+1) = n^3(1+1/n)^3 / (n^5(5(1+1/n)^5+1/(n^5) × n^5(5+1/n)/(n^3)=
=(1+1/n)^3 / ((5(1+1/n)^5+1/(n^5) × (5+1/n)/1
При n→бесконечности а_(n+1)/a_n→1/(5^5)×5/1=1/(5^4)=
=1/625=0,0016<1. то ряд збігається