ответ во вложении Объяснение:
Объяснение:
Квадратное уравнение можно представить в виде:
a(x-x1)(x-x2)=0, где x1 и x2 - корни уравнения;
Раскроем скобки, тогда a*x^2-a*x(x1+x2)+a*x1*x2=0 (1)
у нас выражение x^2-x-p=0 (2)
Если сравнить 2 выражения.
Коэффициент в (2) перед x^2=1, отсюда следует, что в (1) a=1.
(1) принимает вид:
x^2-x*(x1+x2)+x1*x2=0
Сравниваем коэффициенты перед x, получаем
x1+x2=1 (3)
сравниваем свободные члены
-p=x1*x2 (4)
также по условию
x1^2+x2^2=25; (5)
тут 2 варианта, решить систему выше или можно предположить решение;
Предположим, что x1=-4, x2=5;
Тогда удовлетворяются все уравнения условия - (3), (5);
получаем, что p=-(-4)*(5)=20
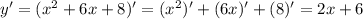
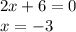
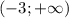, а убывает -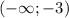 
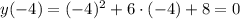
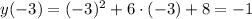- наименьшее
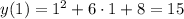- наибольшее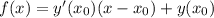
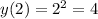
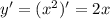
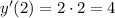
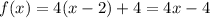
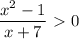
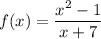
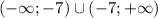
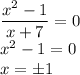
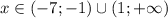
ответ: на фото
Объяснение: