Не все. Надо рассмотреть два случая. Вокруг треугольника можно описать прямоугольник со сторонами параллельными осям координат( границам клеток). Тогда площадь прямоугольника минус площади прямоугольных треугольников - площадь нашего треугольника. Второй случай , когда этого сделать нельзя. Тогда прямоугольник надо провести так, чтобы большая сторона треугольника была диагональю ( вершины треугольника в углах прямоугольника), третья вершина внутри прямоугольника. Тогда из площади большого прямоугольника надо вычесть три треугольника( прямоугольных) и один прямоугольник. Но вывод, естественно, тот же.
Вот решение. Пусть есть такой треугольник. Тогда можно вокруг него дорисовать прямоугольник так. (Сетку дорисуйте сами так, чтобы вешины треуг. были в точках пересечения линий клеток. Нарисуйте на клетчатой бумаге) Площадь клетки есть 1(единица). Тогда площадь нашего треугольника будет "площадь прямоугольника минус площади дополнительных треугольников". Площадь прямоугольника - натуральное число. Площадь любого доп. треугольника будет "основание * высоту /2" И если либо основание, либо высота - четное, тогда площадь - натуральное. Если нечетное- тогда в знаменателе 2. А сумма, разность натуральных с дробными со знаменателем 2 дает дробное со знаменателем 2, а никак не 4. Вот и все.
Дискриминант трехчлена f(x) = ax² + 2bx + c: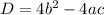 .
.
Дискриминант трехчлена равен
равен 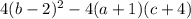
По условию, дискриминант трехчленов f(x) и g(x) равны
Тогда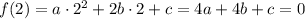
ответ: f(2) = 0.